@SabanSureh : à ta place je n'essaierais pas

Il n'est pas toujours fin l'animal et aujourd'hui il est particulièrement grognon

Vasimolo

@Godisdead : La question ne doit pas être claire ( comme d'habitude ) .

La largeur de la boîte est fixée à 4 , sa longueur est censée correspondre au nombre de tartelettes .

Je vais corrigé dans le message initial .

Vasimolo

On peut : sur le dessin, onloge 6 tartelettes sur moins de 3 fois le diamètre. Combien en moins ? Je ne sais pas, il doit bien y avoir un truc de sinus avec des rac(2) et rac(3)

Il faut juste rattrapper une demi-tartelette de longueur.
Et en gagner une de plus...


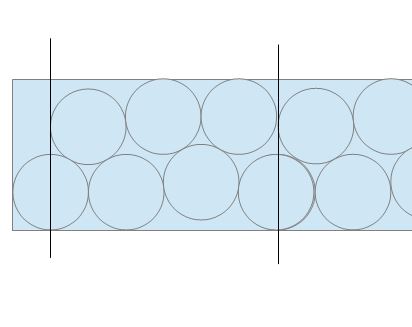
Mais je me lance pour 111 tartelettes..

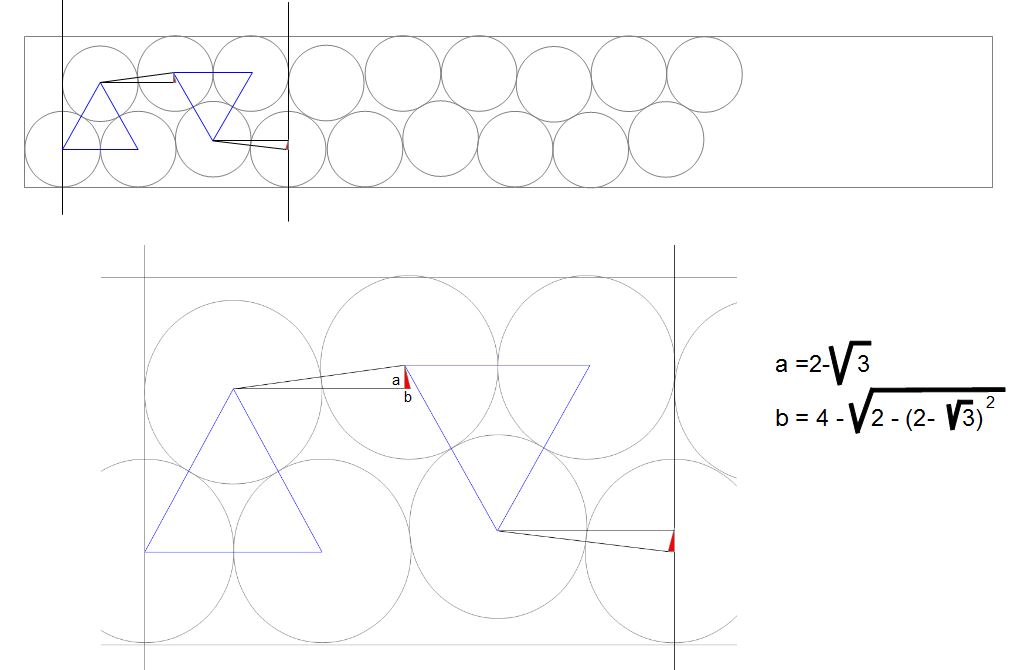
PS 2 et 4 sont intervertis dans la deuxième formule

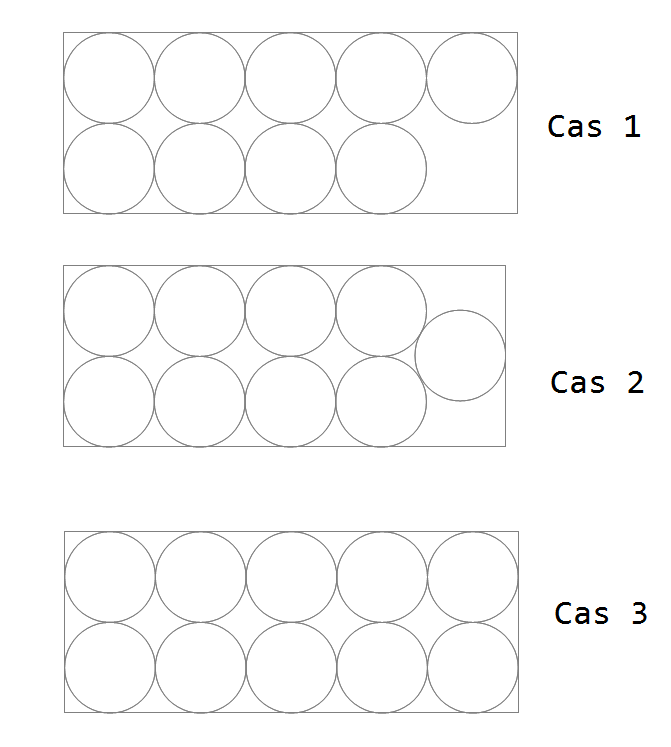
Bon, je vais faire 3 cas :

Cas 1 : le nombre de tartelettes est impair et celui qui range droit est un idiot fini...
J'en range plus que lui dès la cinquième tartelette si la boîte est de taille optimale pour ma méthode.

Cas 2 : Le nombre de tartelettes est impair et il range un peu mieux la dernière...
Cette fois-ci, je ne gagnerai de la place qu'à la 49e tartelette

Cas 3 : c'est celui qui doit être implicite dans l'énoncé , le nombre de tartelettes est pair.

Si la boîte est optimale pour ma méthode, ma 172è tartelette rentrera dans une boîte de 171,97 cm

Si la boîte est optimale pour sa méthode (longueur multiple de 2), dans une boîte de 334cm de long, je pourrai mettre un 335è tartelette qui nécessitera d'atteindre une longueur de 333,99cm

@Gwen : Ton approche est la bonne mais il y a une petite erreur
@Annyo : Au mariage les dimensions de la boîte étaient 4XL . J'ai rêvé ou tu veux  découper les tartelettes du pâtissier en petits morceaux

Vasimolo

Toujours pas de bonne réponse

Je reformule l'énoncé pour ceux qui n'auraient pas compris .

On considère un rectangle de longueur L ( entier ) et de largeur 4 . Est-il possible de ranger sans chevauchement L+1 galettes de rayon 1 dans ce rectangle ? Si oui quelle doit être la longueur minimale du rectangle ?

Bonne recherche .

Vasimolo

Bonjour, est-ce qu'une simple application du théorème de Pythagore est suffisante pour répondre à ta question?

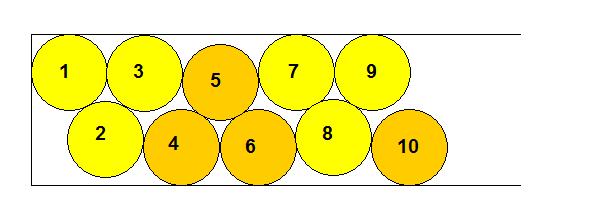
En rangeant les tartelettes comme sur le dessin, on "perd" une demi-tartelette dès le début, mais à chaque changement de couleurs, on gagne un petit chouias (z) de place. Donc au bout d'un certain nombre de tartelettes, on aura récupéré la longueur de la demi-tartelette perdue et 2 fois plus de tartelettes après, on aura "gagné" une demi-tartelette.

Concrètement, dans un repère Oxy plaqué sur les bords bas et gauche de la boite, les coordonnées des centres des tartelettes sont :
x1=1, y1=3
x2=2 et y2 vérifie : (y2-y1)²+(x2-x1)²=2², soit y2=3-rac(3)
x3=3, y3=3
x4 vérifie : (y4-y2)²+(x4-x2)²=2², soit x4=rac(4rac(3)-2)+2.

On va appeler z le chouias gagné : x4=4-z.

On a z=0,01803047....

Toutes les 3 tartelettes, on va à nouveau gagner la longueur z dans la boîte :
x(3n+1)=3n-nz.

Nous recherchons la tartelette i=3n+1 qui vérifiera xi<=i-2 (c'est-à-dire dans une boîte de longueur i-1).
3n-nz<=3n+1-2, soit nz>=1, soit n>=1/z, soit n>=55,46.

Il faut donc n=56, soit i=119 tartelettes pour pouvoir les faire tenir dans une boite de longueur 118.

Conclusion : il y avait du monde au mariage de sa nièce

En relisant ma proposition, je m'aperçois que mes tartelettes 1 et 2 ne servent à rien.
On peut donc les supprimer et mettre 117 tartelettes dans une boite de longueur 116.

Je positionner les tartes comme ci-dessous :



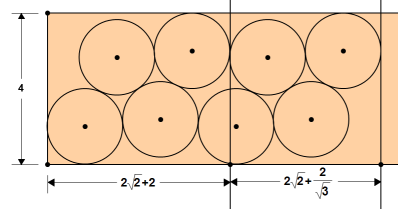
Par groupe de 4, les tartes sont tangentes entre elles. Le premier groupe de 4 tartes nécessite une espace horizontal égal à [latex]2 \sqrt{2}+2[/latex], ensuite chaque nouveau groupe de 4 nécessite un espace horizontal supplémentaire de [latex]2 \sqrt{2}+\frac{2}{\sqrt{3}}[/latex].

Si x est la longueur de la boîte, on peut donc calculer le nombre de tartes contenues dans la boîte avec cette disposition par le calcul suivant :
[TeX]\frac{4 \left(x-2 \sqrt{2}-2\right)}{2 \sqrt{2}+\frac{2}{\sqrt{3}}}+4[/TeX]
Ce nombre devrait valoir x + 1 pour réussir le challenge du pâtissier.

L'équation [latex]\frac{4 \left(x-2 \sqrt{2}-2\right)}{2 \sqrt{2}+\frac{2}{\sqrt{3}}}+4=x+1[/latex] a comme solution [latex]-\frac{3 \left(4+\sqrt{2}-\sqrt{3}\right)}{-6+3 \sqrt{2}+\sqrt{3}}[/latex] c'est à dire environ 436,473

En fait ça fonctionne déjà avec 436.0015 (l'équation ne tenant pas compte de la partie entière de x).

Aire d'une tarte=pi
Pour que le nombre de tarte qu'il est possible de mettre soit supérieur à l, il faut donc que (4l-lpi)/pi>l  or c'est tout le temps le cas car L>pi.

Je ne suis pas sûr d'avoir correctement répondu à la question, mais au moins j'ai essayé !

Même dessin que looser, mais j'ai calculé l'angle par dichotomie. La plus efficace des méthodes est celle qui donnera l'angle de déviation le plus prononcé. Je suis tout de même un peu étonné que la méthode Gwen, Vasi,.. soit plus efficace, car la déviation se produit 2 fois sur 3 au lieu de 2 fois sur 2 comme dans la méthode looser- nodgim. Mais bon l'angle doit sûrement être plus prononcé...

Aussi n'avons nous pas la certitude que la meilleure configuration a été trouvée...

Je trouve comme dylasse pour l'ordre de grandeur, on peut mettre 6 tartelettes tous les 5.963939066.
Chacune occupe en moyenne une largeur de [latex]\frac {1.963939066}6=0.9939898[/latex]
0.9939898(n+1)=n est satisfait pour n = 165.38

Je lui fais confiance pour l'ajustement aux extrémités,
ça doit bien faire environ n=167.