 |
#1 - 15-12-2015 18:41:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 15-12-2015 19:35:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteeau 114
Vasimolo est partout aujourd'hui...
Je dirais tous les rectangles.
On va découper parallèlement à la largeur à l'endroit tel que si "a" est la petite part de la longueur, b la grande part et c la largeur:
a/c=c/b ou ab=c².
Si on pose a+b=L on peut résoudre algébriquement la position de a et b. On peut aussi résoudre géométriquement car je crois me souvenir que a et b sont dans ce cas les 2 segments de la base d'un triangle rectangle au sommet séparés par le projeté de la hauteur c.
#3 - 15-12-2015 19:38:49
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gteau 114
Bonsoir,
Un rectangle de largeur [latex]l[/latex] et de longueur [latex]L[/latex] peut être découpé en deux rectangles semblables différents [latex](l ,x)[/latex] et [latex](l,L-x)[/latex] si [latex]x*(L-x) = l*l[/latex].
Ce n'est possible que si [latex]L>2*l[/latex].
Il existe peut-être d'autres formes, je vais chercher..
#4 - 15-12-2015 19:59:40
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
gâtezu 114
Tous les rectangles dont le ratio des cotés est strictement superieurs à 2.
Prenons un rectangle de dimensions x*y. avec x<y
On calcule c = y/x le rapport des 2 cotés
puis n1 = (c - sqrt( c^2-4 ))/2
et n2 = (c + sqrt (c^2-4))/2
(c'est la ou on voit que c>2 sinon sqrt(c^2-4) est impossible dans R)
On coupe alors le rectangle initial en 2 morceaux:
1er morceau: x par n1*x
2eme morceau: n2*x par x
example:
rectangle de depart: 10 x 25
c = 2.5
n1 = 2.5 - sqrt(6.25-4) = 0.5
n2 = 2.5 + sqrt(6.25-4) = 2.0
le rectangle est coupé en 2 portions de
10 * 20 (avec un ratio de 2 sur 1)
et
10 * 5 (avec un ratio to 2 sur 1)
Les ratios sont les memes, et les tailles sont toujours differentes.
Voila.
Note: avec un ratio initial de 2, on obtient 2 carrés de tailles identiques...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#5 - 15-12-2015 21:59:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 14
Enigmatus prend beaucoup de précautions et il a raison 
Nodgim et Dan s'emballent un peu vite 
Vasimolo
#6 - 15-12-2015 23:42:13
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Gââteau 114
Réponse = n'importe quel gâteau rectangulaire dont la longueur (b) vaut au moins le double de sa largeur (a).
En posant: c1 = (b/2).[1+(1-4a²/b²)^(1/2)] et: c2 = (b/2).[1-(1-4a²/b²)^(1/2)], on aura: c1 + c2 = b et: c2/a = a/c1.
Les deux rectangles: a x c1 et: c2 x a sont bien semblables.
#7 - 16-12-2015 06:12:03
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
Gâteau 1114
Pour un rectangle au moins 2 fois plus long que large, il existe la solution triviale de le découper en deux rectangles (x+1/x >=2).
Pour un rectangle moins long, je ne pense pas.
On peut toujours faire une mise en abyme et jouer avec la notion d' "infini" mais je ne pense pas que ce soit le but...
#8 - 16-12-2015 08:30:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
âGteau 114
Aïe, j'ai été eu !
Oui, il faut tout de même que la longueur soit au moins le double de la largeur.
C'est confirmé aussi par la construction géométrique.
Pour trouver géométriquement l'emplacement de la coupe, on trace depuis le milieu (pte de compas) d'un coté long un demi cercle de rayon moitié longueur, et l'intersection de cet arc avec l'autre coté long est l'endroit où il faut couper. Si la 1/2 longueur est plus petite que la la largeur, il n'y a pas d'intersection.
Il n'y a pas d'autres découpes possibles, mais là c'est un chouïa plus compliqué à démontrer...
#9 - 16-12-2015 09:24:54
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâteai 114
JTout d'abord la séparation ne peut pas couper le rectangle sur des côté adjacents. Sinon les deux figures n'auraient pas le même nombre de sommets et ne pourraient donc pas être homothetiques .
Si la séparation des deux figures n'etait pas un segment parallèle à l'un des côtés du rectangle, les deux figures ainsi formé ne pouraient être homothetiques que vues "tête beche" (par observation élémentaire) ce qui signifie quelle seraient de tailles identiques et ne pourraient donc pas répondre au problème.
Dans le cas où la séparation est un segment parallèle à l'un des côtés du triangle on modélise l'équation d'homothétie à partir du ratio des longueurs (sans oublier les contraintes de cohérence entre les longueurs). On obtient une équation du second degré dont le déterminant impose que la grande longueur soit supérieure à deux fois la petite longueur.
On obtient bien une solution acceptable du point de vue des contrainte dès que l'inégalité strict est respectée
Le critère recherché est donc : L>2×l
#10 - 16-12-2015 09:27:51
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâeau 114
Salut !
Il y a déjà tous les rectangles de côtés a et (a^2 +1) coupés en a^2.
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#11 - 16-12-2015 09:59:17
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâteaau 114
bonjour.
un rectangle de largeur a et de longueur b avec b = ka avec k>2 peut être partagé en 2 rectangles semblables dont le rapport d'homothétie h est
[TeX]h = \frac{k + \sqrt{k^2-4}}{2}[/TeX]
un exemple avec k=3
[TeX]h = \frac{3 + \sqrt{5}}{2} = 2.618034 = 1 + \psi = \psi^2[/TeX]
dans ce cas [latex]\psi[/latex] est le nombre d'or
avec k=2 le rectangle est partagé en 2 carrés égaux.
avec k = 2.1 --> h = 1.370..
#12 - 16-12-2015 18:20:05
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
gâyeau 114
Si le rectangle est de largeur a et hauteur b où a > 2b
alors en faisant un peu de math on trouve une découpe verticale à [latex]\sqrt{a^2-4b^2}/2[/latex] du bord donnant deux rectangles semblables de tailles différentes
Sinon, sans faire de math, on fait ça :
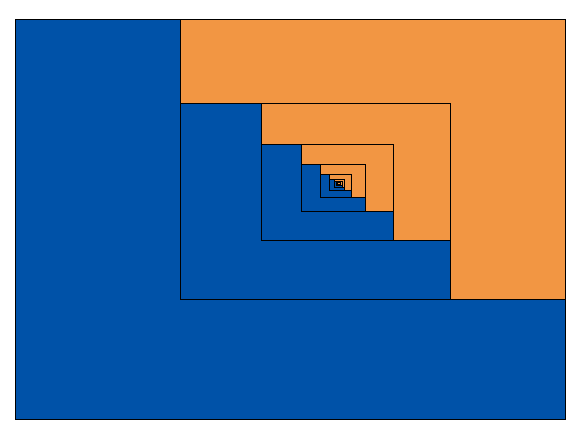
Les rectancles sont semblables.
Et ton pâtissier doit être infiniment talentueux pour le centre 
#13 - 16-12-2015 18:51:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteaau 114
Je n'ai pas tout lu ( il y a beaucoup de monde sur l'affaire et je me disperse trop en ce moment ) .
Ce n'est pas possible si la largeur fait plus que la moitié de la longueur ????
Vasimolo
#14 - 17-12-2015 06:59:48
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâetau 114
Une des parts contient forcément au moins un des 4 angles droits et une portion des côtés adjacents.
Donc l'autre part aussi, puisqu'on a affaire à des homothéties.
Si les parts ne contiennent qu'1 seul des 4 angles droits, cela implique qu'elles sont découpées selon une diagonale. Ce cas ne peut convenir (longueur identique).
Les parts doivent donc contenir chacune 2 des angles droits.
Par définition, une part est une surface contiguë, donc elles contiennent également chacune 1 côté en entier et 2 portions d'autres côtés. Dans le cas d'un découpage non (droit et perpendiculaire), on tombe sur une impossibilité puisque seule une rotation à 180 degrés serait possible mais qu'aucune homothétie n'est alors applicable (même largeur).
Donc il reste le découpage droit et perpendiculaire dont j'ai donné les caractéristiques plus haut. Ces proportions sont uniques et en effet la largeur ne peut pas faire plus que la moitié de la longueur.
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#15 - 17-12-2015 12:29:52
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
gâyeau 114
Salut
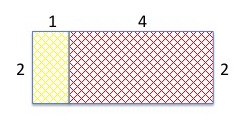

Dimension des gâteaux
Longeur=2,5 largeur
#16 - 17-12-2015 18:09:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gââteau 114
A part Fix et Nobodydy qui vont à la pêche aux gâteaux avec une douce désinvolture  , tous les autres sont convaincus que ce n'est possible que si la longueur fait au moins deux fois la largeur . , tous les autres sont convaincus que ce n'est possible que si la longueur fait au moins deux fois la largeur .
J'ai pourtant sous les yeux un magnifique fraisier assez proche d’un carré et coupé en deux parts semblables et différentes .
Vasimolo
#17 - 17-12-2015 19:22:28
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâteau 1114
Beh non, je suis d'accord avec les autres. 
On est bien d'accord qu'on n'a pas le droit d'avoir une "part Tatin" (retournée) ?
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#18 - 17-12-2015 19:33:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtau 114
Si Fix , la Tatin est autorisée (on dit indirectement semblable chez les non pâtissiers).
Vasimolo
PS : en plus je n'avais pas fait attention que tu avais posté un deuxième message : tu fais donc parti du troupeau des l>2l ( seul Nobodydy va à la pêche  ) )
#19 - 17-12-2015 22:55:49
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
Gtâeau 114
Et ma proposition elle est valide ? 
Je suis à la recherche d'une solution avec un nombre finie de segments, ou une découpe courbe peut être. Je n'ai rien pour le moment.
Je n'ai pas sortie d'argument pour l'impossibilité, je suis un peut vexé d'être mis dans le groupe des |>2| 
#20 - 17-12-2015 23:53:38
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâtea 114
Voici pour le cas d'une découpe en 2 rectangles :
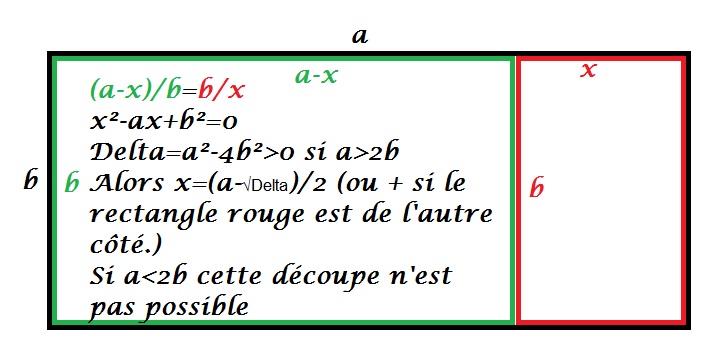
Pour les autres découpes je n'ai pour le moment aucune solution...
#21 - 18-12-2015 08:50:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteu 114
@Mathieu : j'avais bien vu ton dessin ( l'idée est bonne ) mais j'étais resté sur ton commentaire au dessus 
J'ajoute un peu de temps pour la recherche .
Vasimolo
#22 - 18-12-2015 11:06:32
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
gâteay 114
Et un truc de ce genre ???
J'ai juste mis le début de la construction ....
cela fonctionne pour les rectangles L=3/2l
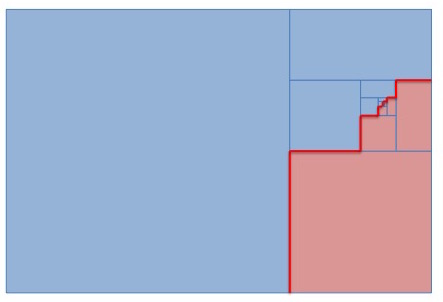
#23 - 18-12-2015 11:33:00
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâteeau 114
bonjour.
avec un gâteau rectangulaire de longueur L et de largeur l
le rapport des côtés du rectangle :
[TeX]\frac{L}{l} = 1+k[/TeX]
le rapport d'homothétie est k
dans ce cas k=0.6823278... est une racine de l'équation:
[TeX]k^3 + k - 1 = 0[/TeX]
on dessine un hexagone concave à 2 marches
avec 2 côtés de plus soit 8 côtés et un rapport d'homothétie de 0.6368829170..
qui est la racine réelle de l'équation:
[TeX]k^5 + k^3 + k - 1 =0[/TeX]
on peut dessiner un octogone concave à 3 marches
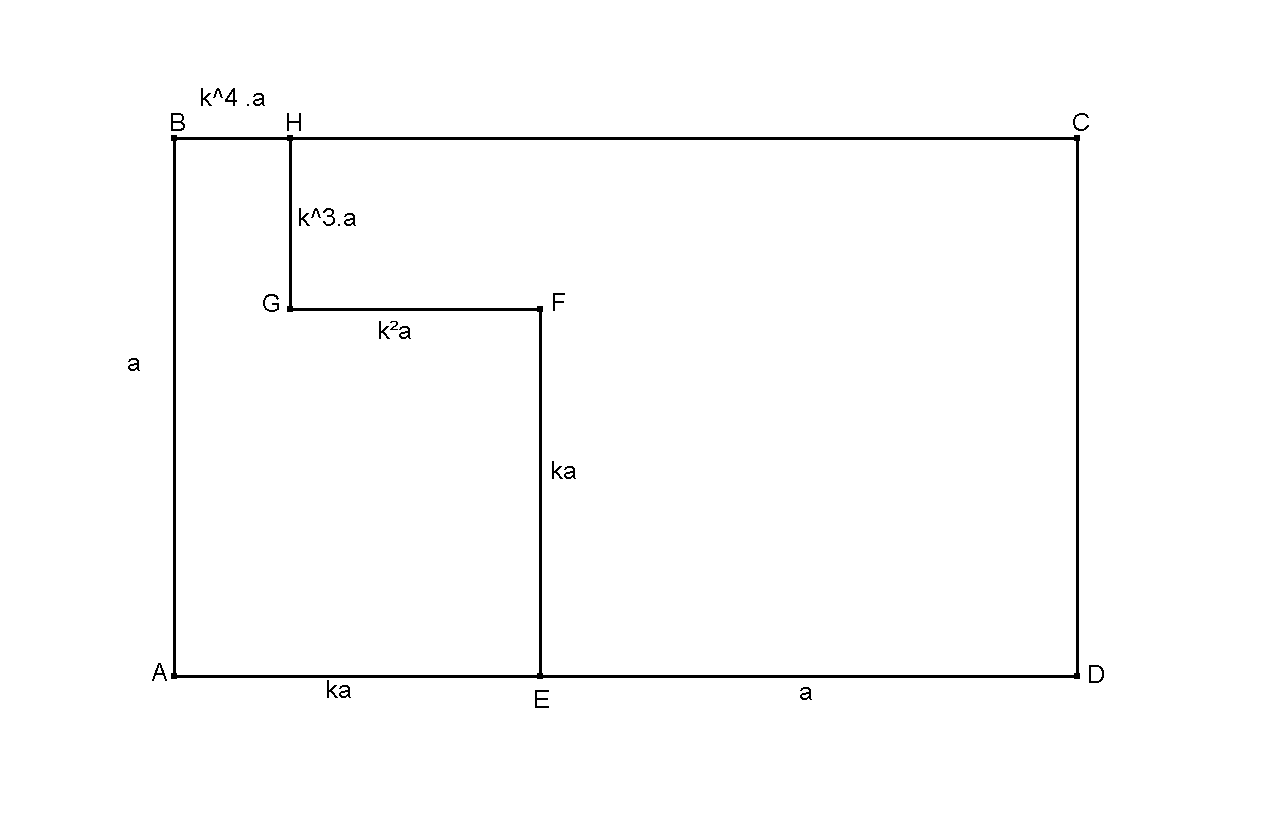
et je rajoute pour être mieux compris :
[TeX] \frac{HB}{GH}= \frac{GH}{GF}= \frac{GF}{EF}=\frac{EF}{ED}=\frac{AE}{CD}= \frac{AB}{CH}=\frac{1}{k}[/TeX]
Aux numérateur , les côtés de la petite part , aux dénominateurs ceux de la grande part. Il y a quand même bien une similitude indirecte de rapport k . Ou je deviens fou. les transformations sont : une symétrie + une homothétie + une rotation de 90° .
Dans ce cas là , une famille de polygones concaves de rapport d'homothétie k
avec le nombre de côtés pour chaque part N = i + 3
k est la racine réelle de l'équation générale où tous les exposants sont impairs:
[TeX]k^i + k^{i-2} + k^{i-4} + ... + k^3 + k - 1 = 0[/TeX]
ainsi avec des parts à 12 côtés , un polynôme de degré 9 , la racine réelle est :
k = 0.6203741812.. et le rectangle mesure a x 1.62037.. a
donc tous ces gâteaux rectangulaire ont pour largeur l = a
et pour longueur L = (1+k) x a
on revient à la figure ci dessus .
avec la longueur on peut écrire :
[TeX]k^4 + \frac{1}{k} = 1 + k[/TeX]
donne l'équation : [latex]k^5 - k^2 - k + 1 = 0[/latex] (1)
avec la largeur on peut aussi écrire :
[latex]k^3 + k = 1[/latex] donnant l'équation:
[latex]k^3 + k - 1 = 0[/latex] (2)
les équations (1) & (2) ont même racine réelle k = 0.6823278038...
#24 - 18-12-2015 12:54:12
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâtau 114
Ca y est, j'ai 
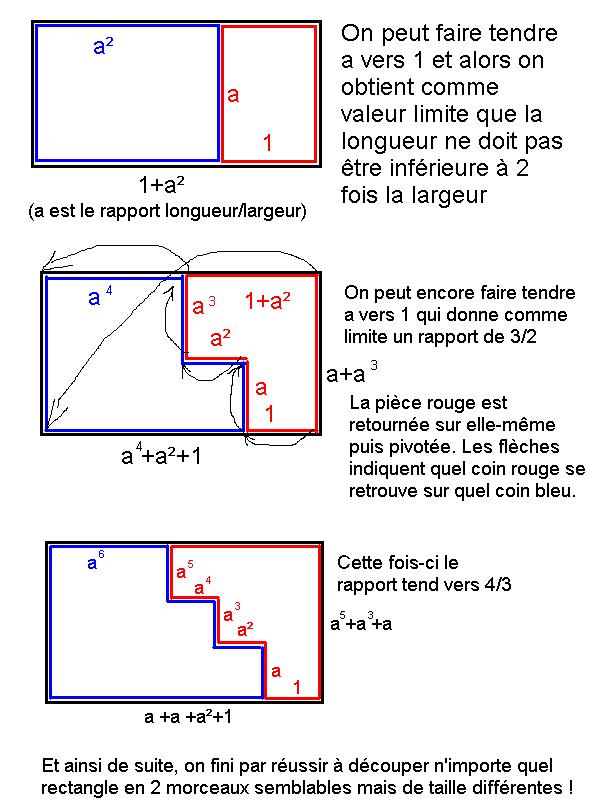
#25 - 18-12-2015 13:15:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtzau 114
Bravo Golgot 
Les autres ne sont pas loin de la solution , encore un petit effort .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum







.png)
.png)




