 |
#1 - 21-03-2014 11:51:00
- Sergent-Bonbon
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 5
La fontaine Romaie
Bonjour ! Je vous propose une petite énigme 
\_/
\_/ \_/
\_/ \_/ \_/
\_/ \_/ \_/ \_/
\_/ \_/ \_/ \_/ \_/
\_/ \_/ \_/ \_/ \_/ \_/
Une fontaine est construite comme le montre le dessin ci-dessus, sur six niveaux.
À chaque niveau, chaque vasque déverse la moitié de son eau dans chacune des
deux vasques situées juste au-dessous d'elle.
La vasque en GRAS(la deuxième en partant de la gauche au niveau inférieur) a
recueilli 1 litre .
Quelle quantité d'eau a-t-on versé dans la vasque supérieure ?
Bon courage :p
#2 - 21-03-2014 13:03:27
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
la fontaine romaone
C'est un triangle de pascal en fait. La quantité d'eau à un niveau sur toutes les vasques égale celle qu'il y avait au niveau supérieur, donc la quantité initiale est égale à celle présente au dernier niveau.
Avec le triangle de Pascal, on a les ratio sur un même niveau.
Au dernier niveau on a donc les ratio 1, 5, 10, 10, 5, 1
La seconde vasque (ratio de 5) contient 1L,
La première vasque contient donc 20 cl, et la ligne totale 6,4 L; qui est la quantité introduite tout en haut.
#3 - 21-03-2014 13:30:41
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
LLa fontaine Romaine
On est bien d'accord qu'une vasque ne commence à se déverser dans deux de celles du niveau inférieur que quand elle est pleine, alors elle déborde.
Les vasques ne commencent pas toutes à déborder au même instant.
Quand elles sont toutes pleines, alors le débit reçu par chacune d'elles obéit au triangle de Pascal.
La vasque en gras ayant été alimentée, on peut en déduire que celle au-dessus à droite a débordé, on ne sait rien sur le niveau de celle au-dessus à gauche.
Car la capacité des vasques n'a pas été indiquée, je crois qu'elle est nécessaire.
#4 - 21-03-2014 14:22:36
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
La fontaine Rmaine
C'est ce que je me suis dit aussi.
Comme c'est pas précisé, j'ai considéré que les vasques devaient être trouées 
#5 - 21-03-2014 17:15:46
- fmifmi
- Passionné de Prise2Tete
- Enigmes résolues : 18
- Messages : 87
La fonatine Romaine
on ne connait pas le volume d'une urne
si V est le volume d'une urne, on a versé 15V+6 litres dans l'urne supérieure
toutes les urnes au dessus sont pleines ( 15 urnes) et il y a 6 urnes inférieures avec chacune 1 litre dedans
#6 - 21-03-2014 17:54:47
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
la fontaine romainr
On nous dit que c'est une fontaine, donc on peut supposer qu'il y a un jet d'eau au fond de chaque vasque qui envoie l'eau en l'air jusqu'à ce que la vasque finisse par se vider. L'eau retombe alors et se répartit équitablement dans les vasques du dessous. J'imagine donc que la solution proposée par Scarta est celle attendue.
#7 - 21-03-2014 18:11:54
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
la fontaine romaibe
"chaque vasque déverse la moitié de son eau"
Que cela est mystérieux! 
#8 - 21-03-2014 18:34:05
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
la fontaine romaone
On peut répondre 15 vasques et 5 litres, une vasque contenant au moins 1 litre.
#9 - 21-03-2014 19:46:52
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
ka fontaine romaine
Je propose de considérer que chaque vasque a une contenance de 1litre et qu'elle déborde uniformément exclusivement dans les vasques de niveau immédiatement inférieur.
#10 - 21-03-2014 19:51:01
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
ka fontaine romaine
PRINCELEROI a écrit:"Chaque vasque déverse la moitié de son eau ..."
"... dans chacune des deux vasques situées juste au-dessous d'elle".
Il faut lire l'énoncé jusqu'au bout: 
#11 - 21-03-2014 20:32:31
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
La fontaine Roaine
PRINCELEROI a écrit:Je propose de considérer que chaque vasque a une contenance de 1litre et qu'elle déborde uniformément exclusivement dans les vasques de niveau immédiatement inférieur.
Sont-elles vide au départ ?
#12 - 21-03-2014 20:41:49
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
la fobtaine romaine
Je propose de considérer que chaque vasque a une contenance de 1litre et qu'elle déborde uniformément exclusivement dans les vasques de niveau immédiatement inférieur et que les vasques sont initialement vides.La source se déversant uniquement dans la vasque supérieure.
Peut-on dire que l'énoncé d'origine était imprécis? 
Edit:pour la réponse voir titou ou scarta ou? pas moi! 
#13 - 21-03-2014 20:46:47
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
la fontaine rolaine
Comme je suis feignant, je verse un mètre cube d'eau et j'aurais 1L dans la vasque en gras !
Ok, je sors ...
#14 - 21-03-2014 20:55:50
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
lz fontaine romaine
Ou alors, l'idée est juste de verser de l'eau dans la vasque du haut, tandis que seule la vasque en gras est vide?
#15 - 21-03-2014 21:06:16
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
L fontaine Romaine
Je pense comme scarta. On verse de l'eau dans le vasque du haut. Cette quantité va se diviser en deux pour remplir les vasques en-dessous. Puis la quantité d'eau de chacun des deux vasques va se diviser en deux pour aller remplir les deux vasques encore en-dessous. Celui du milieu va donc être rempli par les deux vasques. Etc ...
#16 - 21-03-2014 21:15:46
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
La fontaien Romaine
Si tu verses 3l seul 2l vont remplir les vasques inférieures et ça complique !
#17 - 22-03-2014 10:14:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
La ontaine Romaine
On peut aussi dire que dans la vasque supérieure, on n'a versé que l'eau nécessaire pour la remplir, tout le reste étant expulsé dans les vasques inférieures...
#18 - 22-03-2014 11:55:57
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
la fontaune romaine
godisdead a écrit:PRINCELEROI a écrit:Je propose de considérer que chaque vasque a une contenance de 1litre et qu'elle déborde uniformément exclusivement dans les vasques de niveau immédiatement inférieur.
Sont-elles vide au départ ?
Je suis assez d'accord.
(V=1 litre est évidemment un minimum, comme l'a indiqué nodgim).
Si V est plus grand, alors les marges commencent à déborder plus tard par rapport aux vasques centrales et le résultat devient autre.
Pour résumer, je propose :
Les vasques ont un volume V=1 litre et sont vides au départ, et pour simplifier, et sans perte de généralité, celle du haut reçoit 1 litre par seconde.
Pendant la première seconde, la vasque du haut est la seule à se remplir.
A partir de t=1, elle reste pleine, les 2 vasques du second étage (compté à partir du haut) mettent 2 s à se remplir chacune à 0.5 litre/s, rien d'autre ne se passe.
A partir de t=3, ces 3 vasques restent pleines, les vasques du 3ème étage commencent à se répartir 1 litre par seconde dans les proportions 0.25, 0.50, 0.25.
La vasque centrale se remplit de t=3 à t=5, les latérales se remplissent de t=3 à t=7.
A t=5, la vasque centrale de l'étage 3 commence à déborder vers l'étage 4
A t=7, les deux vasques latérales de l'étage 3 commencent à déborder vers l'étage 4.
Et ainsi de suite...
Un petit graphique peut aider.
En fin de compte, je trouve 23.
EDIT 65/3 soit environ 21.67
Latex encore en panne
#19 - 22-03-2014 13:32:44
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
La foontaine Romaine
Et l'évaporation dans tout ça !? 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#20 - 23-03-2014 09:19:13
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
ka fontaine romaine
halloduda a écrit:Un petit graphique peut aider.
Voilà  : :
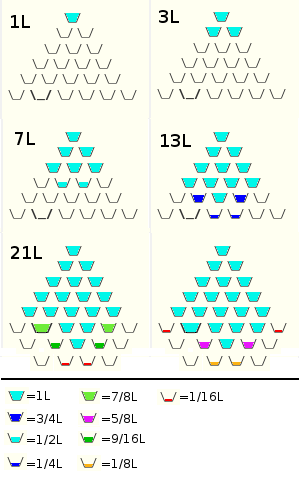
Ce qui donne en fin de compte :
21 + 2* (1/16 + 5/8 + 1/8) = 21 + 13/8 L = 22L + 5/8L = 181/8L
ça fait un peu moins que les 23L proposés par halloduda, mais il y a peut-être des étapes que j'ai mal fait.
Il y a sûrement plus simple.
#21 - 23-03-2014 10:05:34
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
la dontaine romaine
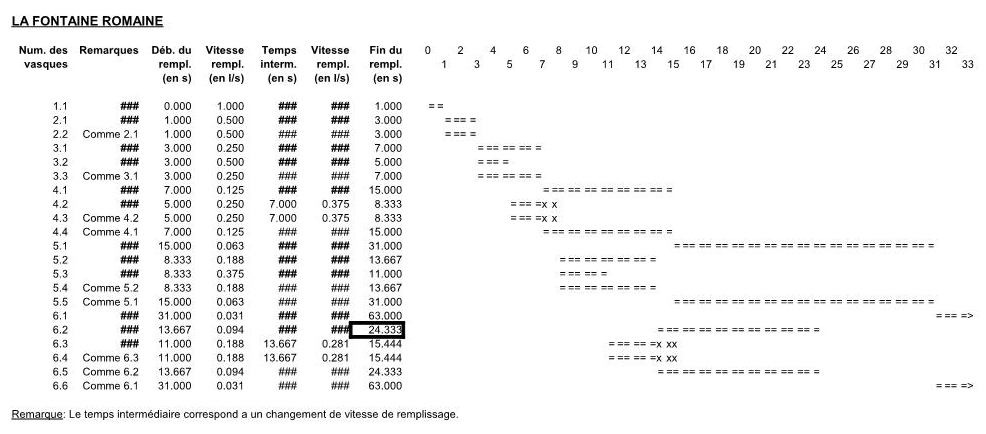
(image zoomable)
Je trouve 30,2 73/3 (soit env. 24,333) litres, mais j'ai dû me tromper quelquepart je ne suis toujours pas sûr de mon coup. 
#22 - 23-03-2014 11:22:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
La fontaine Romaie
On doit pouvoir trouver des tas de variantes à ce problème très amusant 

Vasimolo
#23 - 23-03-2014 12:18:54
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
La fontaine Romainne
Je trouve précisément 22 litres.
Je ne prends en compte que les vasques ayant un effet!
En partant de 22l il arrive 10.5l n2 puis 4.75l et 9.5l n3 puis 1.875l et 6.125l n4 puis sans effet et 3l n5 et 1l dans la vasque concernée.
#24 - 29-03-2014 21:12:30
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
La fontaine Rmaine
Après vérification, j'ai 21L + 5/8L.
J'explique à partir de la position obtenue après 21L que j'ai recopié ci-dessous.
(avec le même code de couleur) :
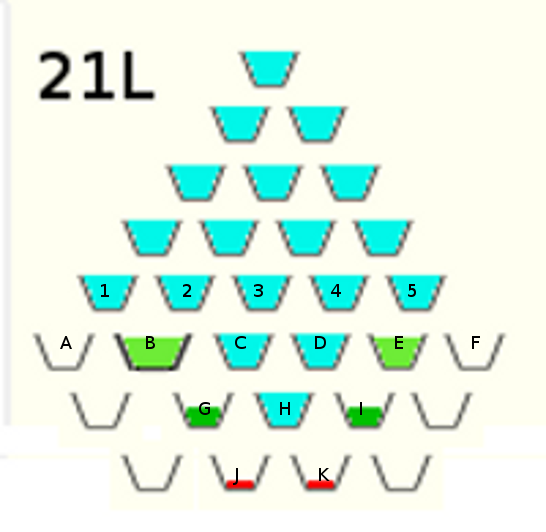
Les vasque supplémentaire sont là pour "récupérer" l'eau qui coule après le sixième niveau.
On s'arrête quand la vasque B est rempli. Cette vasque est déjà rempli aux 7/8.
Donc B est rempli quand on elle a reçu 1/8L
Elle reçoit 1/8L des vasques 1 et 2, cela signifie que chacune des vaques numéroté de 1 à 5 déborde de 1/16L de chaque côté.
i) Ainsi les vasques A et F reçoivent 1/16L et les vasques B, C, D et E reçoivent 1/8L.
ii)Donc les vasques B et E se remplissent.
Les vasques C et D étant déjà pleines redistribuent le huitième de litre qu'elles ont reçu en débordant de 1/16L de chaque côté.
iii)Donc les vasques G et I reçoivent 1/16L supplémentaire
La vasque H reçoit 1/16 + 1/16 = 1/8L, mais comme elle est déjà pleine elle redistribue ce huitième de litre en débordant elle aussi de 1/16L de chaque côté.
iv)Donc les vasque J et K reçoivent 1/16L supplémentaire.
Donc pour récapituler :
On a les 15 vasque pleines des 5 premiers étages plus les 3 vasques C, D et H qui était déjà pleine. Ce qui fait 18 vasques pleines.
-D'après ii) les vasques B et E sont également pleine, on arrive donc à un total de 20 vasques pleines (ce qui fait donc 20L).
-D'après i) Les vasques A et E contiennent chacune 1/16L ce qui fait en tout 1/8L. On en est donc à 20L + 1/8L.
-Les vasques G et I contenaient déjà chacune 9/16L et d'après iii) elles ont reçu chacune 1/16L, elles contiennent donc chacune 9/16 + 1/16 = 5/8L.
ce qui fait en tout 10/8L = 1L + 2/8L.
On en est donc à 20L + 1/8L + 1L + 2/8L = 21L + 3/8L
Les vaques J et K contenaient déjà chacune 1/16L et d'après iv) elles ont reçu chacune 1/16L, elles contiennent donc chacune 1/16 + 1/16 = 1/8L.
ce qui fait en tout 2/8L.
Nous avons donc au final : 21L + 3/8L + 2/8L = 21L + 5/8L.
En fait une manière plus rapide de voir ça est que chacune des 5 vasques du cinquième niveau à déborder de 1/8L donc quelque soit la manière dont cela se propage ensuite on a au total 21L + 5 * 1/8L = 21L + 5/8L.
Il y a sûrement plus simple.
#25 - 29-03-2014 22:19:47
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
La fontaine Romane
Moi, je trouve 22+5/8L. Mais j'ai fait étape par étape, du coup, je peux me tromper.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










