Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 10-08-2011 11:05:08#0 Pub#2 - 10-08-2011 18:05:32
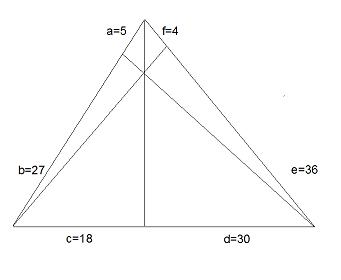
Triange de DiophanteUn triangle de longueur de côtés 32, 40 et 48 semble convenir. #3 - 10-08-2011 19:15:14
TTriangle de DiophanteD'accord Rivas. #4 - 11-08-2011 17:13:32#5 - 12-08-2011 08:10:10#6 - 12-08-2011 11:20:21
triangle de diiphanteJe n'ai pas vraiment cherché au hasard... J'ai surtout tatonné pour trouver une équation que puisse résoudre Wolfram alpha. #7 - 13-08-2011 13:24:44
truangle de diophanteMerci aux participants. Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.