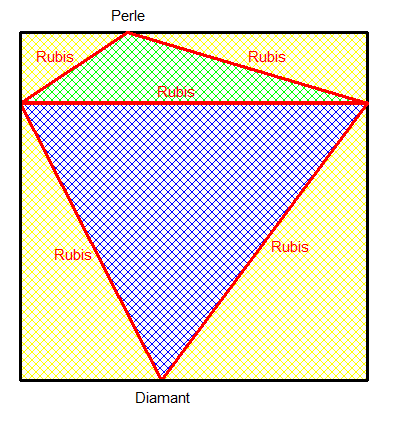
|
#1 - 23-12-2016 19:08:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 23-12-2016 21:50:24
- shadokpoilu
- Habitué de Prise2Tete
- Enigmes résolues : 45
- Messages : 26
fâteau 130
Bonjour,
je me mets en mode bourrin (il y a peut-être plus subtil)
j'appelle c le côté du carré,
je note x la distance entre le bord gauche et le diamant,
y la distance entre le bord gauche et la perle
et h la distance entre la ligne de partage et le bas.
grâce au théorème de Pythagore, on doit donc minimiser :
[TeX]\sqrt{x^2+h^2}+\sqrt{(c-x)^2+h^2}+\sqrt{y^2+(c-h)^2}+\sqrt{(c-y)^2+(c-h)^2}(+ c \mbox{ qui ne changera pas...}) [/TeX]
étant donné que les longueurs sont bien sûr positive, on peut éliminer les racines carrés et en développant, on obtient :
[TeX]x^2+h^2+c^2-2xc+x^2+h^2+y^2+c^2-2ch+h^2+c^2-2cy+y^2+c^2-2ch+h^2[/TeX]
j'ai enlevé le c final...
j'isole les éléments en h qui sont finalement les seuls qu'on peut minimiser :
[TeX]4h^2-4ch[/TeX]
une telle fonction de h est minimum pour h = c/2
Donc finalement, la seule chose à faire est de placer la ligne de séparation au milieu du gâteau.
Shadokpoilu.
#3 - 24-12-2016 07:57:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteua 130
Salut Vasimolo.
Pas tout compris dans le problème. La ligne parallèle est imposée, mais le quadrilatère rouge, non ? Le dessin fait il partie du cahier des charges ?
#4 - 24-12-2016 10:00:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 1130
@Shadockpoilu : attention [latex](\sqrt{a}+\sqrt{b})^2\neq a+b[/latex] 
@Nodgim : il faut trouver un moyen simple de positionner la ligne horizontale qui va minimiser la longueur du tracé rouge . Les positions de la perle et du diamant sont imposées .
Bonne recherche .
Vasimolo
#5 - 24-12-2016 12:31:57
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
gâteay 130
Salut,
Sauf erreur il faut placer la ligne horizontale au milieu du gâteau 
Le périmètre d'un triangle est donné par :
[TeX]f: (c,x,h) \mapsto \sqrt{x^2+h^2}+\sqrt{(c-x)^2+h^2}[/TeX]
pour un gâteau de coté [latex]c[/latex], un triangle de hauteur [latex]h[/latex] et dont le sommet est à l'abscisse [latex]x[/latex]
Ensuite [latex](\frac{\mathbb{d}f}{\mathbb{d}h})(c,x,h)-(\frac{\mathbb{d}f}{\mathbb{d}h})(c,y,c-h)=0 \Leftrightarrow h=c/2[/latex]
#6 - 24-12-2016 12:42:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteu 130
Tu arrives à la même conclusion que Shadockpoilu . Un résultat aussi simple devrait pouvoir se justifier sans sortir l'artillerie lourde .
C'est une question que je me pose aussi 
Vasimolo
#7 - 24-12-2016 18:34:05
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Gâteeau 130
Salut,
Effectivement le résultat est simple puisqu'il faudra toujours placer G et C aux milieux de [AF] et [BE].
Pour cela on peut créer une fonction f avec pour inconnue x=AG=BC
Une fois que cette fonction est créée on la dérive et on obtient :
f'(x) = 4(2x-AB)
f'(x) = 0 pour x=AB/2
f est décroissante sur [0;AB/2] puis croissante sur [AB/2;AB]
Le minimum est donc atteint pour x=AB/2
Mais je sais que tu adores les réponses géométriques, j'attendrai avec impatience ta soluce.
#8 - 25-12-2016 12:44:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtea u130
Tu risques d'être un peu déçu , on obtient la réponse analytiquement et il y a sûrement une subtilité géométrique qui l'explique mais elle m'échappe pour le moment : avis aux amateurs 
Et bien sûr : Joyeux Noël à tous !
Vasimolo
#9 - 25-12-2016 19:07:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Gâetau 130
Si tu penses à 1/2, c'en est très proche , mais je doute que ce soit la réponse exacte sans symétrie dans la figure.
#10 - 25-12-2016 23:23:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 30
Je ne pense à rien de plus qu'à une stratégie permettant d'optimiser les gains à moindre effort , après , on peut tenter le juste prix .
Vasimolo
#11 - 26-12-2016 19:57:08
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1426
- Lieu: Nicastro / Tronville
Gtâeau 130
j'étais un peu étonné de lire que la réponse était simple.
puis rassuré par la réponse de gwen27
(je pensais me planter comme dhab)
Celle-ci dépend en effet de la position du diamant et de la perle
et n'est au milieu que pour des positions symétriques du diamant et de la perle.
cf le fichier qui permet de modifier les paramètres de la situation
et de voir le minimum pour les différentes positions
(un bouton donne le coeff de réglage fin pour le trait parallèle)
https://ggbm.at/EEBbsb2k
bon tout à vous ... depuis la Tchéquie
Lélio Lacaille - Du fagot des Nombreux
#12 - 26-12-2016 20:22:28
- Rene13
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 1
Gâteau 310
Je suis nouveau sur le forum, bonjour à tous 
Je n'ai pas la solution analytique!
Calcul du périmètre avec Pythagore (idem Shadokpoilu)
On obtiens une fonction F(h) (h est l'inconnue) à minimiser.
Donc calcul de la dérivée par rapport à h pour trouver le zéro de la dérivée.
Le problème est que l'équation finale (très lourde!) n'est pas résoluble! (par moi)
Mais la réponse h = c/2 n'est pas bonne dans le cas général (non symétrique).
Il suffit d'un contre exemple, par exemple si c= 1, x = 0, y = 0.5 le minimum est à 0.48!
Donc à mon avis pas de solution simple.
Hâte de voir la réponse 
et merci pour ces belles énigmes
René
#13 - 27-12-2016 08:03:16
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteu 130
Perso, j'attendais aussi la vue des réponses pour me rendre compte de ce qui a été dit, les réponses de Vasimolo me troublant beaucoup.
La longueur des segments peut en effet se faire par Pythagore, et si on pose que le carré est de coté 1, la hauteur de la ligne horizontale x, alors on a une longueur de segment de la forme V(a² + x²) ou V(a² + (1-x)²).
En calculant la dérivée (il ne faut pas essayer de résoudre cette équation analytiquement ! ), qui vaut x / V(a² + x²) ou (x-1) / V(a² + (1-x²)), on se rend compte qu'il s'agit tout simplement du cosinus de l'angle, ou son opposé.
Pour être précis : En bas du carré, au point diamant, les 2 angles des segments par rapport à la verticale sont ceux dont la dérivée donne un cosinus positif. Au point perle en haut, les 2 angles des segments avec la verticale sont ceux dont la dérivée donne un cosinus négatif. Le minimum de longueur est atteinte lorsque la somme des cosinus positifs est égale en valeur absolue à la somme des cosinus négatifs. Cela se produit quand la ligne est vers le milieu, dans une fourchette 0,53 / 0,47 environ.
Il est à noter que si on voulait trouver le mini de longueur pour un seul chemin de la perle au diamant, celle ci est conforme avec l'égalité des cosinus et correspond au principe du rebond de la boule de billard pour l'angle entre les 2 segments.
#14 - 27-12-2016 09:37:54
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1426
- Lieu: Nicastro / Tronville
âGteau 130
Merci nodgim pour ce développement
(j'ai cherché un peu du côté des relations au niveau des angles mais ne suis pas parvenu à tes résultats.)
Petite précision
(?)
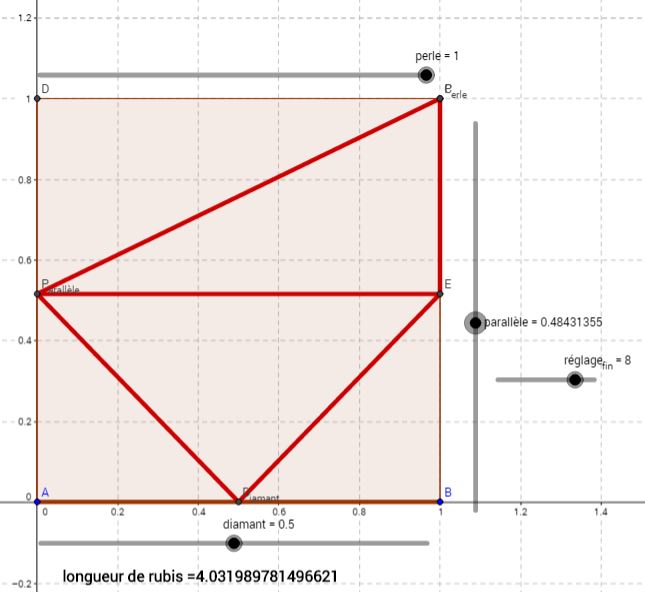
où l'on voit la valeur approximative qui correspond à
perle à une extrémité et diamant au milieu (ou le contraire)
d'où l'écart entre les deux extrêmes
(dans le cas d'un carré de 1 sur 1)
(à vérifier sur la figure animée https://ggbm.at/EEBbsb2k )
Lélio Lacaille - Du fagot des Nombreux
#15 - 27-12-2016 10:36:42
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
hâteau 130
Vu Aunryz. En fait, ce n'est pas le décalage max. J'ai obtenu un 0,4763 pour perle en 0,5 et diamant en 0,1.
#16 - 27-12-2016 23:04:27
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1426
- Lieu: Nicastro / Tronville
Gtâeau 130
Effectivement
n'est-ce pas une singularité ?
Pour diamant en 0.5
Il semble que le décalage maximal corresponde
pour perle à 0.5
à une valeur légèrement inférieure à 0.1 (j'aurais eu tendance à croire à 0) pour diamant.
Sinon,
pour répondre aux besoins du pâtissier,
"La position de la perle et du diamant ne lui sera communiqué qu'à la dernière minute , il devra alors finaliser son œuvre rapidement .
Un petit coup de main pour aider mon pâtissier à bien finir l'année ?????"
Je l'engage à utiliser l'outil de géométrie dynamique mis à sa disposition
Avec une petite déception peut-être
la différence de rubis entre la solution banale
trait au milieu
et l'optimale (au maximum un écart de 2,5cm sur un gâteau d'1m de côté)
ne lui fera gagner au plus qu'un rubis
...
me semble-t-il.
(7/10 mm sur 3953 mm de longueur de rubis)
bon tout aux participants
et à Vasimolo
Le pâtissier qui nous a offert ce sujet de flexion.
Lélio Lacaille - Du fagot des Nombreux
|
 |

 Accueil
Accueil
 Forum
Forum