|
#1 - 27-12-2015 11:26:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 27-12-2015 16:53:58
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
gâyeau 116
La réponse est oui on peut toujours effacer les marques.
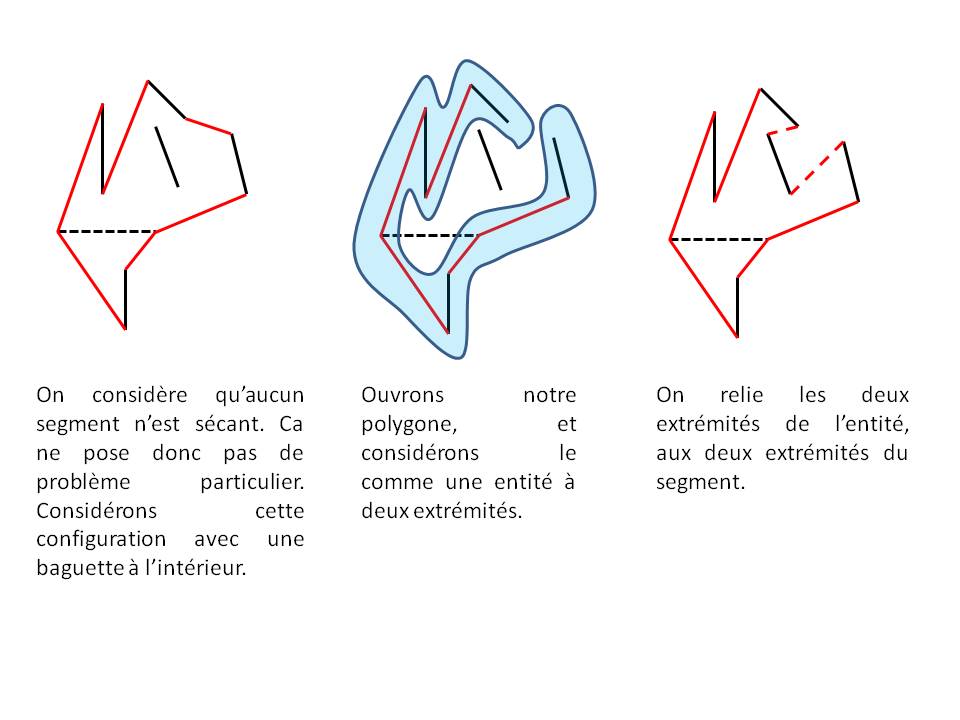
On passe un fil rouge élastique autour de l'ensemble des segments bleus. Certains segments bleus sont confondus avec le fil rouge d'autres non. Ceux qui ne le sont pas ont une extrémité sur le fil rouge, l'extrémité à l'intérieur du polygone délimité par le fil rouge. Soient E1 E2 E3, 3 sommets consécutifs du polygone rouge, et E4 tel que E2-E4 est un segment bleu. On tire sur le fil rouge en E2 et on l'amène en E4. Le polygone suit alors dans cet ordre les pts E1 E2 E4 E3. Entre E4 et E3, ce n'est pas forcément une ligne droite, il peut y avoir des pts intermédiaires E5, E6...extrémités de segments bleus. A toute extrémité Ea atteinte par le fil rouge, on peut donc amener le fil rouge par ce procédé à l'autre extrémité Eb du segment bleu. Quand chaque extrémité des segments bleus est atteinte par le fil rouge, il peut rester à l'intérieur du polygone des segments bleus isolés. Parmi ces segments bleus isolés, il y en a forcément qui sont accessibles par le fil rouge, c'est à dire qu'on peut faire un triangle (segment de fil rouge-l'extrémité du segment bleu isolé). On réalise cette opération de triangulation autant de fois que nécessaire, en privilégiant tjs l'avancée du fil rouge le long d'un segment bleu (on a atteint une extrémité d'un segment bleu ---> on rejoint l'autre extrémité).
Pour faire simple, c'est comme ci on devait relier des pts par un polygone, ce qui est élémentaire, mais avec cette contrainte que certaines liaisons entre pts sont obligées. En procédant comme indiqué, ça ne pose aucune problème.
Il existe des tas de solutions possibles, dans les configurations compliquées, selon le choix qu'on fait pour l'endroit de l'avancée du fil rouge.
#3 - 27-12-2015 21:57:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 1166
@Nodgim : je ne comprends pas comment tu places ton fil rouge au départ , il me semble qu'il n'y a aucune raison qu'il soit en contact avec chacun des segments bleus .
Vasimolo
#4 - 28-12-2015 07:16:52
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtea u116
Mon montage marche bien, c'est après que ça se gâte, avec la triangulation.
Un contre exemple, il me semble:
...X...................................................X
...X...................................................X
...X...................................................X
...X...XXXXXXXXXXXXXXXXXXXXXX....X
...X...................................................X
...X...................................................X
...X...................................................X
...X...................................................X
...X................XXXXXXX.....................X
...X...................................................X
...X...................................................X
...X...................................................X
...X...................................................X
...X...................................................X
...X...XXXXXXXXXXXXXXXXXXXXXX....X
...X...................................................X
...X...................................................X
...X...................................................X
#5 - 28-12-2015 07:48:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteai 116
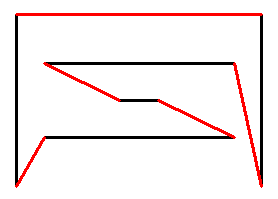
Il me semble que ton contre-exemple n'en est pas un :
Vasimolo
#6 - 28-12-2015 14:49:59
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
Gâteau 16
De façon intuitive, avec 3, et 4 baguettes, je déduis facilement que pour trois points non-alignés, la chose est toujours possible.
Il suffit de trouver une figure qui réponds au problème pour n baguettes et d'en appliquer le schéma à toutes figures contenant n baguettes initialement, peu importe l'orientation des baguettes.
Mais je n'en apporte aucune démonstration formelle. Je sens que la récurrence est valable pour tout n, mais existe-t-il une démonstration et est-ce elle que l'on cherche?
La résolution de ce problème exige-t-elle des connaissances mathématiques élevées?
#7 - 28-12-2015 16:21:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâetau 116
@Laidzep : le problème n'utilise pas de résultats mathématiques au-delà des connaissances du lycée 
Vasimolo
#8 - 28-12-2015 16:59:43
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
Gâteau 1166
Encore une question. Le but est-il d'en enfermer un maximum, ou de montrer qu'il est toujours possible d'en enfermer au moins un?
#9 - 28-12-2015 17:14:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtteau 116
Le but est que le lacet à 2n sommets enferme l'ensemble des n segments initiaux .
Vasimolo
#10 - 28-12-2015 17:52:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gââteau 116
Si j'ai donné un contre exemple faux, c'est parce que l'algo que je proposais n'est pas efficace.
La solution ne passerait elle pas par une récurrence ?
#11 - 28-12-2015 17:54:19
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
#12 - 28-12-2015 18:09:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâreau 116
D'accord , il y a mésentente sur les termes : je considère qu'un segment est dans le polygone s'il n'en sort à aucun endroit ( il peut être complètement contenu dans la frontière ) .
Vasimolo
PS : Nodgim , bien joué mais je ne donne pas d'indice pour le moment 
#13 - 28-12-2015 18:12:41
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
Gââteau 116
Ok. Ca me parait clair, maintenant. J'ai une idée, je vais encore réfléchir à sa pertinence en testant quelques exemples. Par contre, j'ai un peu de mal à voir une démonstration rigoureuse.
#14 - 28-12-2015 18:49:14
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
gâyeau 116

Que ma démonstration est laborieuse...
#15 - 28-12-2015 18:57:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtezu 116
Le problème Laidzep , c'est que les nouvelles baguettes ajoutées peuvent être à l'intérieur du polygone déjà construit et là , c'est le début des ennuis 
Vasimolo
#16 - 28-12-2015 19:11:47
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
#17 - 28-12-2015 19:17:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#18 - 28-12-2015 19:22:00
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
Gâteauu 116
On peut mettre les baguettes dans des endroits bien plus singuliers lollol
Humm... On pense vraiment à la même chose... 
Plus sérieusement, sauf à chevaucher les baguettes, je ne vois pas ce qui pourrait poser problème.
#19 - 28-12-2015 19:31:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 116
Je te laisse y réfléchir 
Vasimolo
#20 - 28-12-2015 20:28:36
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
Gâteau 11
Les baguettes peuvent-elles se chevaucher?
#21 - 28-12-2015 21:33:53
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâyeau 116
Peux on tenter une enveloppe convexe qui ne touche pas toute les baguettes ou est ce interdit ?
#22 - 28-12-2015 21:53:02
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
Gâteau 11
J'ai beau me creuser la tête, je ne vois rien qui puisse perturber la configuration.
C'est possible avec deux baguettes. Et par extension, avec 3, et plus...
Même avec plusieurs baguettes à l'intérieur comme ci-dessous.
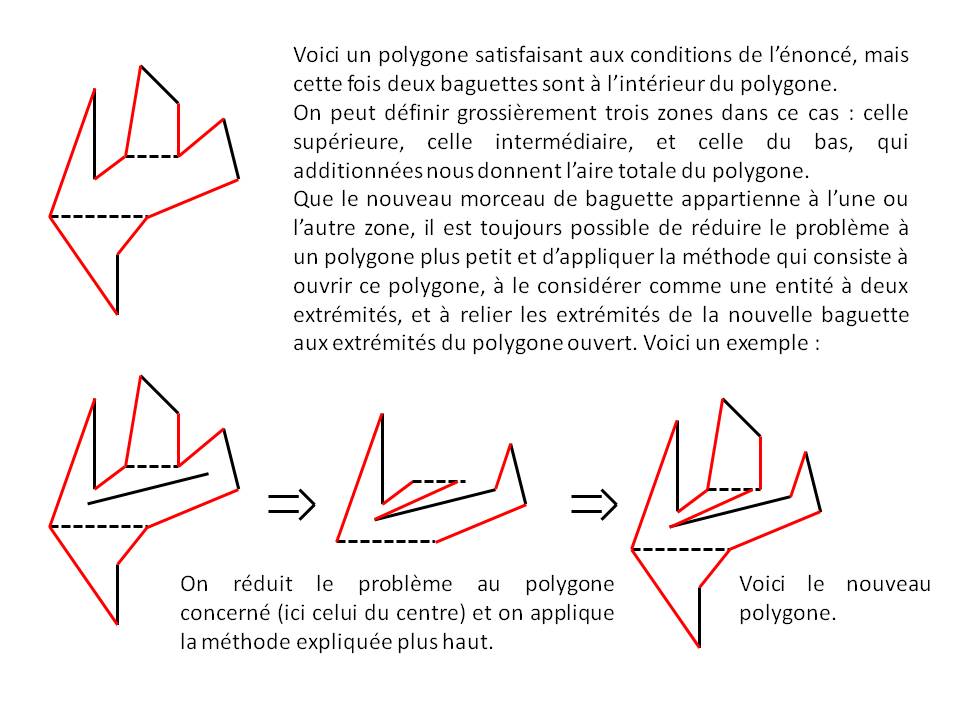
Et, pour une baguette à l'extérieur, je ne vois pas de problème particulier.
Bref, j'oublie peut-être quelque chose mais je ne vois pas quoi pour l'instant.
#23 - 28-12-2015 23:02:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âteau 116
@Portugal : l’enveloppe convexe ne touche pas forcément toutes les baguettes mais les sommets de la boucle doivent être ceux des baguettes .
@Laidzep : tous tes exemples sont bien sûr corrects mais illustrer n’est pas démontrer .
Vasimolo
#24 - 29-12-2015 02:29:20
- Laidzep
- Professionnel de Prise2Tete
- Enigmes résolues : 35
- Messages : 165
Gâteau 1166
Je pense aux démonstrations informulées, qui peuvent être rigoureusement exact, la mienne étant probablement trop approximative pour être qualifiée comme tel.
Je vais tenter une démonstration plus formelle, même si la méthode illustrée que je proposais plus haut s'étend à tout type de polygone (même ceux avec plusieurs baguettes complètement enfermées à l'intérieur de la figure).
Soit deux segments [AB] et [A'B'] du plan, de tel sorte qu'il n'existe pas trois extrémités alignés.
Il est possible d'associer par paire les extrémités des deux segments (A et A', B et B', ou A et B', et A' et B), de tel sorte qu'en reliant ces extrémités, on obtienne un polygone à 4 sommets.
2 baguettes pour 4 sommets.
On peut initialiser une récurrence pour le cas n = 2.
D'après l'exemple donner en exemple dans l'énoncé, il est également possible d'initialiser la récurrence pour n = 3.
Il existe donc au moins une configuration qui répond aux exigences de l'énoncé.
Posons donc l'hypothèse comme vraie : pour une configuration à " n " baguettes, on peut construire le polygone à " 2n " sommets.
Peut-on vérifier l'hérédité au rang n+1?
Pour le cas n+1, et d'après l'hypothèse posée, on peut nécessairement construire un polygone à " 2n " sommets conforme aux exigences de l'énoncé, et garder de côté un segment [A'B'] du plan, disjoint du polygone.
En supprimant un côté de ce polygone à " 2n " sommets, on obtient une entité géométrique constituée de " 2n-1 " segment, " 2n-2 " sommets, et possédant deux extrémités que l'on nommera A et B.
Par un raisonnement analogue à l'initialisation de la récurrence, on reliera par deux segments les extrémités citées A et B à celle du segment [A'B'] disjoint du polygone.
On obtient alors un polygone à " 2n-1+3 " côtés, soit " 2n+2 " côtés, et à " 2n-2+4 " sommets, soit " 2n+2 " sommets, c'est-à-dire " 2 (n+1) " sommets.
Pour une configuration à " n+1 " baguettes, on a donc " 2 (n+1) " sommets.
L'hérédité est vérifiée.
Il est donc toujours possible de construire un polygone qui satisfasse aux conditions de l'énoncé.
Je ne trouve aucun contre-exemple qui viendrait contrarier ce raisonnement, pour le moment.
Soyez indulgent, c'est une tentative un peu hasardeuse, mais je ne vois pas vraiment comment l'exprimer d'une façon différente avec les outils mathématiques que je possède.
#25 - 29-12-2015 11:30:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtezu 116
@Laidzep : désolé je ne suis toujours pas convaicu par ta démonstration 
J'ai l'impression que tu fais marcher ta récurrence à l'envers . Le fonctionnement "normal" serait : on part d'une configuration de n+1 segments , on retire un des segments ( il faut préciser lequel si le choix a une importance ) et on explique comment intégrer le (n+1)ème segment au polygone à 2n côtés existant par hypothèse de récurrence .
Par exemple , on enlève le segment bleu ci-dessous et on relie les segments noirs comme indiqué .
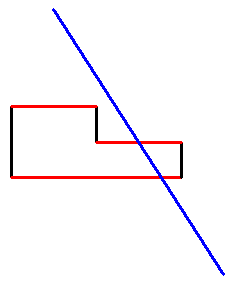
Par quelle méthode associes-tu le segment bleu au polygone déjà construit ?
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum