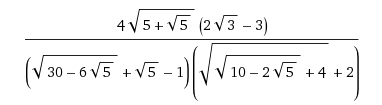|
#1 - 16-02-2016 19:02:17
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
4 polygones emboîîtés
Une énigme qui devrait vous rappeler une énigme récente, j'aime bien le recyclage décidément...
À l'intérieur d'un triangle équilatéral de côté 1, je construis un carré, le plus grand possible.
À l'intérieur de ce carré, je construis un pentagone régulier, le plus grand possible.
À l'intérieur de ce pentagone régulier, je construis un hexagone régulier, le plus grand possible.
Et puis c'est tout !
Question : trouver la plus grande valeur possible pour le côté de l'hexagone.
Question subsidiaire, pour départager les gagnants : exprimer cette valeur avec les 4 opérations et le moins de symboles "racine carrée" possible.
Je précise d'avance, pour m'éviter d'avoir trop mal au crâne, que je vous fais cadeau de la démonstration de l'optimalité de votre solution (si jamais elle n'était pas optimale, tant pis pour vous : vous prendriez le risque de vous faire battre par un concurrent).
Bonne recherche !
#2 - 16-02-2016 20:32:28
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
4 polyones emboîtés
Pour eviter les [latex]\sqrt{n}[/latex], peut-on ecrire [latex]n^{1/2}[/latex] ?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#3 - 16-02-2016 21:20:04
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
4 polgyones emboîtés
Non, dhrm77, tu es un odieux tricheur  La puissance ne fait pas partie des "4 opérations". La puissance ne fait pas partie des "4 opérations".
#4 - 17-02-2016 19:05:02
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
4 polygones embboîtés
@halloduda : je trouve moins que toi, me serais-je trompé ? Peux-tu poster une figure pour que j'en aie le coeur net ?
#5 - 17-02-2016 20:48:42
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
4 pilygones emboîtés
J'ai adopté un processus qui m'a conduit à un résultat... ce résultat est-il optimal? Je ne saurai être catégorique, néanmoins j'en donné un arrondi numérique. Si c'est bon alors je le mettrai. côté hexagone = 0.2063816
#6 - 17-02-2016 20:50:02
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
4 pollygones emboîtés
@halloduda : je pense que ton résultat est encore un poil trop grand.
@kossi_tg : pas mal du tout, mais on peut faire un chouïa mieux.
#7 - 17-02-2016 22:26:48
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
44 polygones emboîtés
A chaque étape, il faut determiner la configuration optimale d'un polygone dans un autre.
Soit:
- T, le coté du triangle
- C, le coté du carré
- P, le coté du pentagone
- H, le coté de l'hexagone
Il y a 2 facons de mettre un carré dans un triangle..
1) le carré à plat (un coté du carré coincide avec un coté du triangle).
2) le carré sur la pointe (un angle du carré coincide avec un angle du triangle).
La meilleure solution est facile à calculer, et c'est la premiere avec [latex]C = (2\sqrt{3}-3) T[/latex]
Il y a aussi 2 facons de mettre un pentagone dans un carré.
1) le pentagone à plat (un coté du pentagone coincide avec un coté du carré).
2) le pentagone sur la pointe (un angle du pentagone coincide avec un angle du carré).
La meilleure solution, ici, est la 2eme. mais alors que la premiere solution est facile a calculer, la 2eme l'est beaucoup moins...
Apres 3 ou 4 essais et 8 pages de calculs, je trouve ...
[TeX]P = \sqrt{2 (4-\sqrt{2 (5+\sqrt{5})})} C[/TeX]
Il y a également 2 facons de mettre un hexagone dans un pentagone.
1) un coté de l'hexagone coincide avec un coté du pentagone.
2) un angle de l'hexagone coincide avec un angle du pentagone.
Je ne sais pas encore laquelle est la meilleure....
à suivre..
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#8 - 17-02-2016 22:56:14
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
4 polygonnes emboîtés
@dhrm77 : de bons débuts, rien a redire pour l'instant. Si ce n'est que bien sûr, on peut faire mieux que 15...
#9 - 17-02-2016 23:53:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#10 - 18-02-2016 00:00:17
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
4 polygones emboîés
Et une bonne réponse pour Vasimolo, avec 9 racines carrées en tout !
#11 - 18-02-2016 07:43:35
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
4 polygone semboîtés
Reprise après corrections.
Graphiquement, je trouve 0.2081187
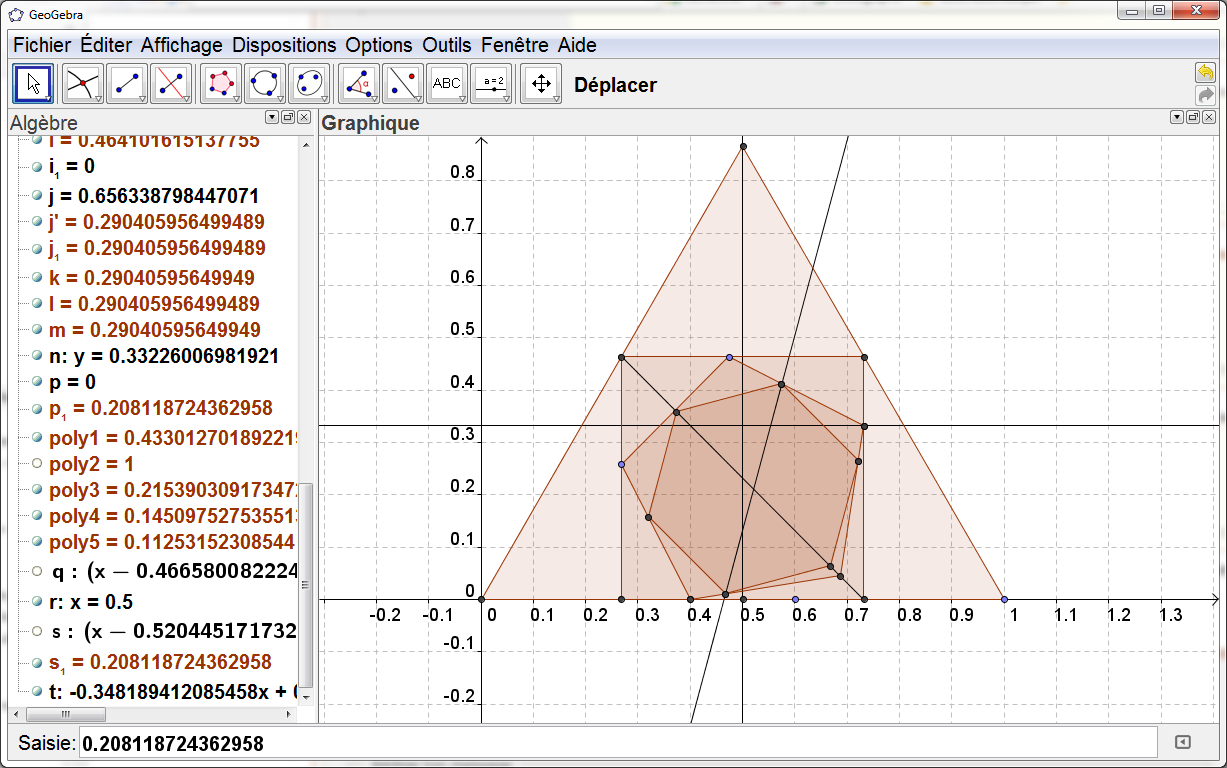
Je renonce aux calculs
#12 - 18-02-2016 11:25:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
4 polygones emboîts
@halloduda : très belle figure, et tu as la bonne valeur numérique, bravo ! Tu as encore le temps pour les calculs, ils sont un peu techniques mais il n'y a pas de raisonnement très compliqué.
#13 - 22-02-2016 22:25:58
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
4 polygonnes emboîtés
Félicitations aux participants ; à Vasimolo, évidemment, pour sa bonne réponse, mais aussi à halloduda pour sa figure, ou à dhrm77 pour son début de démonstration.
Son message de dhrm77 donne en effet les deux premières étapes. Quant à l'hexagone inscrit dans le pentagone, on trouve que [latex]H=\frac{(\sqrt{5}+1)\sqrt{5+\sqrt{5}}}{2(\sqrt{2}+\sqrt{3}\sqrt{5+\sqrt{5}})}P[/latex].
Tout ça se fait avec de la bonne grosse trigonométrie bien épaisse, mais sans subtilité particulière.
#14 - 22-02-2016 23:09:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#15 - 25-02-2016 01:50:55
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
4 polygonse emboîtés
Je propose la même chose dans l'espace avec des polyèdres irréguliers dont le rapport du cube de la somme des longueurs par la moyenne au carré de la surface des deux polyèdres qui "l'entourent" est égale au tiers du volume du polyèdre considéré 
Je précise que j'avais juste envie de la sortir et qu'il n'y a rien d'arrogant ou de méprisant ou quoique ce soit d'autre dans ce que je viens de dire ! 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum