Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 13-07-2016 22:46:12
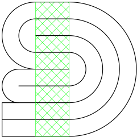
origami pour les nylsUn classique qui n'est pourtant pas sur le forum :
#0 Pub#2 - 13-07-2016 22:57:10#3 - 14-07-2016 00:09:22
Origami pour les nul@gwen27 : #4 - 14-07-2016 03:47:45
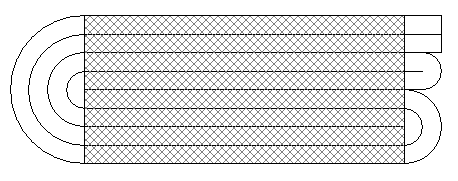
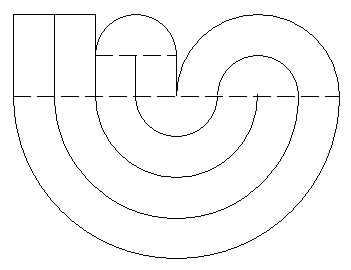
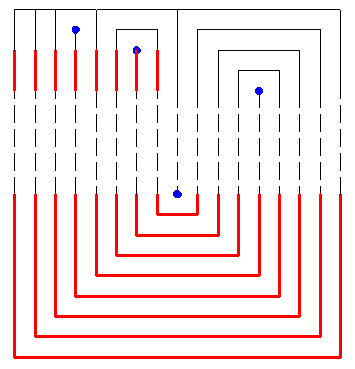
orihami pour les nulsTrouvé sur le web: #5 - 14-07-2016 09:56:40#6 - 14-07-2016 10:55:58#7 - 14-07-2016 12:04:07#8 - 14-07-2016 12:18:49
Origami pour les nullsTout dépend si plier en 2 signifie #9 - 14-07-2016 12:27:59#10 - 14-07-2016 16:51:41
Origami pourr les nulsL: longueur de la feuille #11 - 15-07-2016 11:19:34
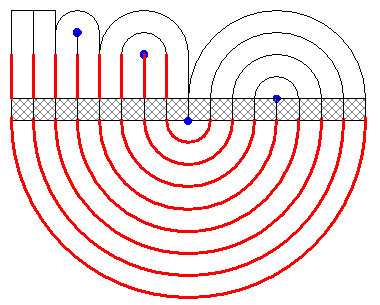
origami pour les nylsJe dois faire une erreur logique quelque part car je n'arrive pas à me débarrasser du terme correctif ( même si je n'avais pas proposé le bon ) : #12 - 16-07-2016 08:35:06
Origam ipour les nulsSalut Sydre, #13 - 16-07-2016 15:13:42#14 - 17-07-2016 00:12:29#15 - 17-07-2016 16:13:25
Origami pur les nulsEn fait dans le lien donné par Franky1103 on considère que "plier en deux" se fait en alignant les centres des demi-cercles : il n'y a donc pas de terme correctif. #16 - 17-07-2016 17:58:33
origami poyr les nulsJolie solution Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.