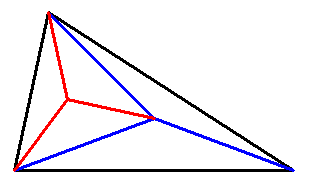
Sans trop de souci, on en trace un depuis un sommet, ce qui est toujours possible.
Puis on coupe le triangle restant en tirant une hauteur.



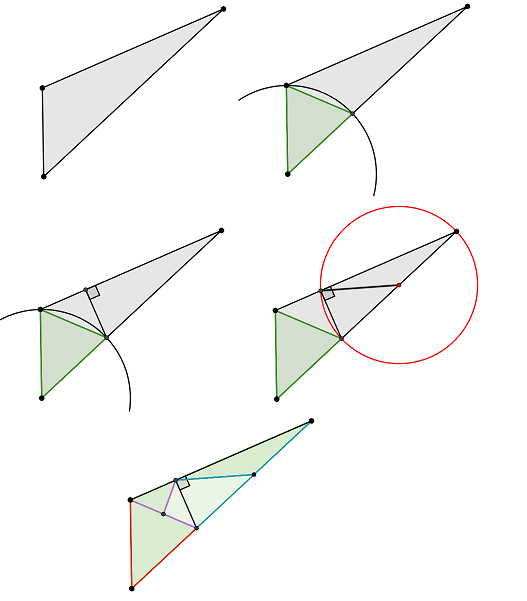
Il y a aussi la version "centre du cercle circonscrit" répétée 2 fois, s'il est interne au triangle...

Eventuellement, le cas particulier du triangle équilatéral :

Pour un triangle à angles aigus, on sait que les trois hauteurs sont concourantes. J'obtiens donc trois sous-triangles isocèles. Je procède de même avec l'un d'entre eux et j'ai ma décomposition en cinq triangles isocèles.

Pour un triangle avec un angle obtus, les trois hauteurs sont toujours concourantes, mais à l'extérieur du triangle. Et c'est là la vraie difficulté du pâtissier. Je réfléchis encore et je reviendrai plus tard.

bonjour.

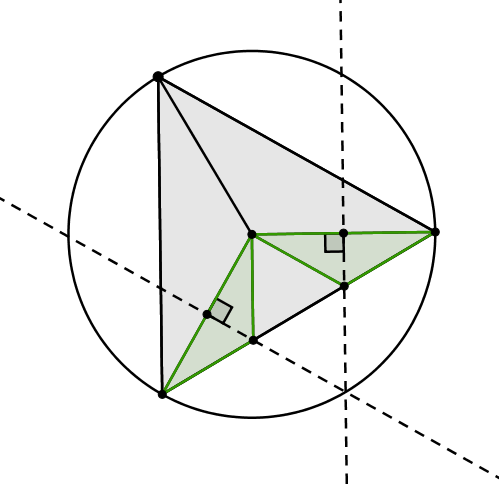
Je pense qu'avec un triangle acutangle , il suffit de tracer 4 médiatrices , ainsi
les 2 points tracés et un des 3 sommets du triangle d'origine sont alignés ;
nous obtenons bien 5 triangles isocèles par construction avec les 6 segments internes .

Oui :

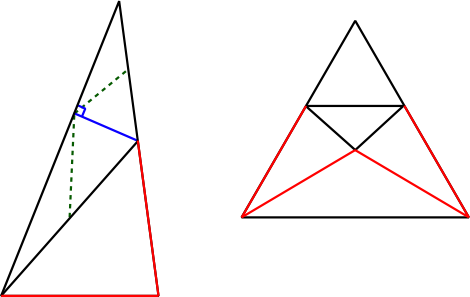
La figure de gauche présente le cas d'un triangle non équilatéral. On reporte la longueur du côté le plus petit (en rouge) sur un des autres côtés strictement plus grand, et voici un premier triangle isocèle. Il reste un triangle quelconque : on trace une hauteur strictement interne à ce triangle (il en existe au moins une), ce qui donne deux triangles rectangles, chacun étant décomposable en deux triangles isocèles.

Si le triangle est équilatéral, cette méthode ne marche pas, mais la deuxième figure présente une façon de s'en tirer.

Oui en effet ce n'est pas méchant. On peut toujours tracer d'abord 2 petits triangles isocèles à partir d'un coté donné, et de sorte qu'il reste un triangle à partager en 3 isocèles, et ça, ça se fait par le point de concours des médiatrices.

re.

avec un triangle rectangle , une première part ( la moitié du gâteau quand même )
et les 4 autres identiques avec un mini triangle de Sierpinski .

il reste le triangle obtusangle .

re.

et enfin pour le triangle obtusangle , je trace la hauteur issue de l'angle obtus .
j'obtiens 2 triangles rectangles à partir desquels , je trace pour chacun la médiane issue de l'angle droit , à ce moment j'obtiens 4 triangles isocèles dont 2 sont obtusangles . Je prend alors l'un d'eux et je trace les 2 médiatrices des côtés égaux
qui vont s'avérer être symétriques par rapport à la bissectrice de l'angle obtus . Ces 2
médiatrices coupent le côté opposé en 2 points , sommets de mon cinquième triangle .Son troisième sommet est le sommet commun à ses 2 voisins .
Dans ce cas là 2 triangles isocèles sont égaux.

@vasimolo :

effectivement je ne sais plus compter.
je crois que j'y suis .
ABC est obtusangle en A et AB est le petit côté .
  je trace la hauteur AH .
Puis je trace le symétrique AB' du petit côté AB par rapport à cette hauteur
j'obtiens un premier triangle isocèle BAB' ; je supprime cette hauteur qui ne me sert plus à rien.  Il me reste un triangle isocèle BAB' + un obtusangle B'AC à partir duquel je trace la hauteur B'H . Pour terminer je trace respectivement les médianes
HD & HE des 2 triangles rectangles AHB' & CHB' . Je viens de construire les 4 triangles isocèles manquants .

@Unecoudée : ça marche , mais il reste quand même un cas particulier qui ne rentre dans aucune de tes catégories ( mais non je ne suis pas pénible )

Vasimolo

la quatrième famille , je pense au triangle équilatéral ABC
G est le centre de gravité à partir duquel je trace 3 triangles GAB , GBC & GAC .
Je prend un des 3 triangles GAB par exemple . Je trace les médiatrices de GA et de GB
Elles coupent AB en 2 points D & E  . Les 5 triangles GAC , GBC , GDA , GEB & DGE
sont isocèles .

Tout a été dit .

Merci aux participants

Vasimolo