 |
#1 - 23-12-2017 13:00:56
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
sangaki
Bonjour à tous,
voici une tentative de Sangaku, représenté avec Geogebra :
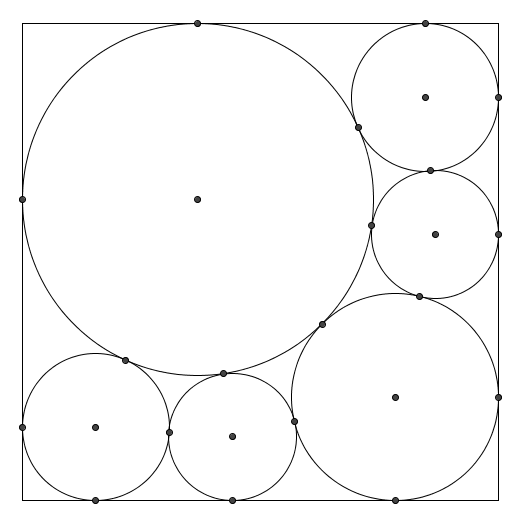
La figure est un carré de côté 1. Les points marqués sont les centres des cercles, ou des points de tangence.
Le but du jeu est de déterminer les rayons des cercles.
Dans un premier temps, il faut trouver un système d'équations vérifié par les rayons, système devant avoir une unique solution ; on pourra se satisfaire d'une solution numérique. Les plus motivés pourront chercher la valeur exacte de ces rayons, c'est possible mais loin d'être évident.
Bon amusement 
#2 - 24-12-2017 09:09:53
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3236
- Lieu: Luxembourg
Sangakuu
J'arrive à démontrer sans difficulté que la somme des deux plus grands rayons (sans utiliser les deux paires de petits cercles) vaut 2-V2. Les autres formules deviennent rapidement inextricables. Quant à la recherche d'une valeur numérique des rayons, ce n'est pas mon truc.
Affaire à suivre et bonnes fêtes à tous.
#3 - 24-12-2017 17:21:30
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
sanhaku
@Franky1103 : si elles sont inextricables au début, c'est normal. Une bonne partie du travail consiste à les simplifier le plus possible afin de réussir à en tirer quelque chose.
Je parlais d'une valeur numérique histoire de dire : quand on a des équations, si un solveur type wolframalpha arrive à calculer des approximations des solutions, c'est bon signe. Mais le but ultime est bien d'obtenir les valeurs exactes, ce qui nécessite sans doute d'abord de simplifier l'écriture des équations.
#4 - 25-12-2017 12:04:04
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Sanggaku
Bonjou,
Intéressant, mais pas évident en effet. Je n'ai pas trouvé la solution exacte.
Notations :
C1 : cercle en haut à gauche
C2 : cercle en haut à droite
C3 : cercle au milieu à droite
C4 : cercle en bas à droite
Les centres sont respectivement O1, O2, O3, O4, et les rayons r1, r2, r3, r4
J'obtiens ces relations :
r2 = ( 1-sqrt(r1) )**2
r4 = 2-sqrt(2)-r1
r3 = ( (1-r2-r4) / (2*(sqrt(r2)+sqrt(r4))) )**2
Et en calculant de 2 façons différentes la distance de O3 au côté supérieur du carré :
r2+2*sqrt(r2*r3) = r1+sqrt(2*(r1+r3)-1)
J'ai fait varier r1 pour que l'égalité précédente soit vérifiée.
Résultat numérique, à comparer avec la solution exacte :
r1 = 0.368699562024
r2 = 0.154286844660
r3 = 0.133974596216
r4 = 0.217086875603
#5 - 25-12-2017 21:52:37
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Snagaku
@enigmatus : bravo  Je trouve les mêmes relations que toi, et les mêmes valeurs numériques. Il te reste à trouver les solutions exactes, ça ne nécessite pas de connaissance théorique plus compliquée que le discriminant d'une équation du second degré, mais les calculs sont méchants. Je trouve les mêmes relations que toi, et les mêmes valeurs numériques. Il te reste à trouver les solutions exactes, ça ne nécessite pas de connaissance théorique plus compliquée que le discriminant d'une équation du second degré, mais les calculs sont méchants.
#6 - 26-12-2017 12:29:36
- Bastidol
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 152
sangzku
Voilà voilà j'ai corrigé (enfin je pense)
[TeX]R4+R3+2*\sqrt { 2R3+2R4-1 } -1\quad =\quad 0\\ R4+R2+2*\sqrt { R4*R2 } -1\quad =\quad 0\\ R4+R1+\sqrt { { (R4+R1) }^{ 2 }-{ (R3+2*\sqrt { R3*R1 } -R4) }^{ 2 } } -1\quad =\quad 0\\ R3+R2+2*\sqrt { R3*R1 } +2*\sqrt { R1*R2 } -1=0\\ [/TeX]
[TeX](R4+R2)*(1+\sqrt { 2 } )\quad -\sqrt { 2 } =\quad 0\quad [/TeX]
Après c'est trop pour mes vieux neurones 
#7 - 26-12-2017 16:28:44
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Sanagku
@Bastidol : un bon début, mais il reste à faire un peu de travail. Tes relations 2, 4 et 5 sont justes. Les relations 1 et 3 sont fausses, car ce qui convient pour la relation 2 ne convient pas pour celles-ci.
Par conséquent il te manque une relation pour terminer la première partie de l'énigme. Bon courage 
#8 - 26-12-2017 18:01:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3838
sangaju
Salut Ebichu,
Je ne me suis pas désintéressé du problème, mais ne suis pas allé au bout, de crainte des erreurs de calcul....
Soit C1 le grand cercle, C2 celui qui lui est diagonalement opposé, C3 celui en bas à gauche et C4 entre C2 et C3. Les 2 autres cercles sont inutiles pour la démo gràce à la symétrie.
On établit un repère orthonormé d'origine le coin bas gauche du carré. On donne à ce carré le coté 1 comme mesure.
Soit Rx rayon du cercle x. Les équations sont établies en utilisant au maximum Rx plutôt que x ou y comme coordonnées des centres des cercles.
Les équations sont établies en définissant de 2 façons différentes les distances entre les centres des cercles :
- D'une part le carré des différences des x et y des coordonnées des centres des cercles.
- D'autre part, le carré de la somme des 2 rayons des 2 cercles concernés.
On aboutit alors à 5 équations à 5 inconnues
(1) : (R1-R3) ² + (1-R1-R3) ² = ( R1 + R3 ) ²
(2) : (R1 - 1 + R2) ² + (1 - R1 - R2) ² = (R1 + R2) ²
(3) : (R3 - x4) ² + (R3 - R4) ² = (R3 + R4) ²
(4) : (R1- x4 ) ² + (1 - R1 - R4 ) ² = ( R1 + R4 ) ²
(5) : ( 1 - R2 - x4 ) ² + ( R2 - R4) ² = (R2 + R4) ²
On note que seul x4 subsiste en coordonnée directe.
(2) donne la relation simple : R1 + R2 = 2 - V2
(1) donne la relation R3 = (1 - VR1) ²
(3) donne la relation x4 = R3 + 2 V(R3R4)
(4) donne la relation x4 = R1 + V( 2R1 + 2R4 - 1 ) le +, à arbitrer car l'une des 2 solutions du second degré, est donné par le dessin.
(5) donne la relation x4 = 1 - R2 - 2 V (R2R4), le - de 2 V... est donné par le dessin.
L'égalité des 2 premières expressions de x4, en remplaçant R3 par f(R1) dans la relation (1) permet de donner R1 en fonction de R4
R1 = ( ( 2 R4 + 1 + 3 VR4) / (4R4 + 1 + 4 VR4) ) ²
L'autre égalité issue de 2 autres expressions de x4 est malheureusement plus compliquée, elle permet d'établir une nouvelle relation entre R1 et R4. A moins d'une erreur.
#9 - 26-12-2017 19:15:56
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Sangak
@nodgim :
En bas à gauche, je suppose ?
Je suis d'accord avec tes relations, sauf la (5). Je suppose que c'est une coquille, et que tu as malencontreusement remplacé un x4 par un R4.
Je pense que de tes 5 équations de départ, on doit pouvoir déduire les 5 inconnues, donc c'est bon pour la 1e partie de l'énigme. A noter que les autres (dont moi-même) n'utilisent pas x4 et se contentent des rayons.
Pour la 2e partie, je suis d'accord avec les 5 relations que tu en déduis, mais pas la toute dernière entre R1 et R4 (mais je peux me tromper). Bon courage pour la suite.
#10 - 26-12-2017 19:31:34
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Sangak
@Bastidol : c'est mieux. Je ne comprends pas d'où vient la relation 1, il me semble qu'elle est fausse. La relation 2 est juste si tu remplaces "R2" par "R3". Les relations 3, 4, 5 sont correctes. Si tu te contentes des relations 2, 3, 4, 5, cela suffit et la première partie de l'énigme est finie 
#11 - 27-12-2017 01:56:23
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
sabgaku
Salut !
J'espère que je suis clair, je ne suis pas allé plus loin pour l'instant, et j'espère aussi que mes équations sont bonnes... (l'image est zoomable)
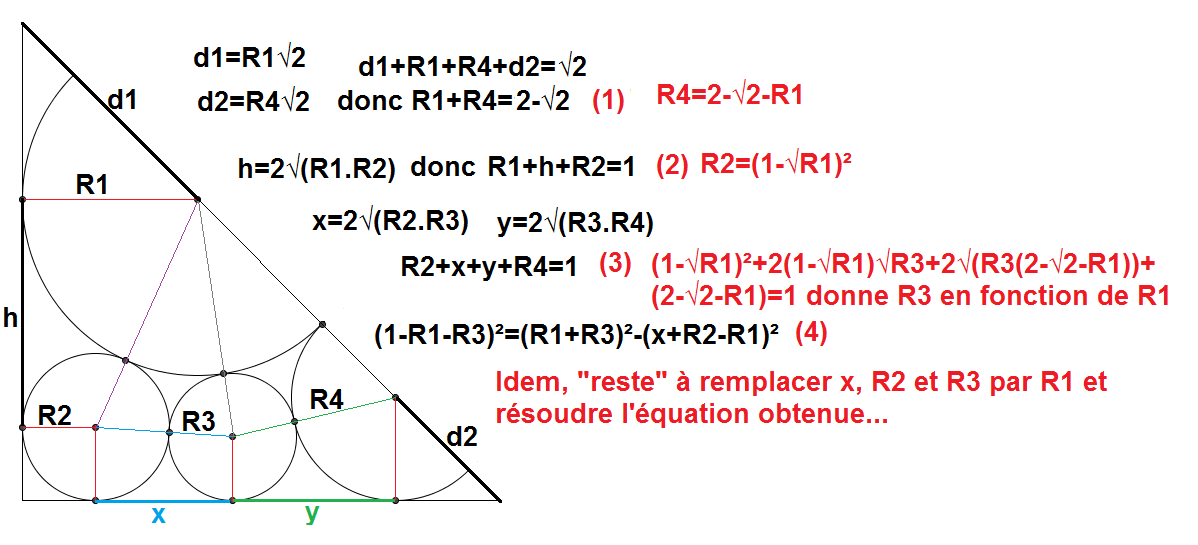
#12 - 27-12-2017 12:24:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
SSangaku
@golgot59 : pour l'instant c'est bon  Tu en es au même point que les autres, il faudrait maintenant résoudre le système que tu as obtenu, et c'est là que les ennuis commencent... Tu en es au même point que les autres, il faudrait maintenant résoudre le système que tu as obtenu, et c'est là que les ennuis commencent...
#13 - 28-12-2017 15:45:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Sanngaku
C'est terminé, merci aux participants. Trouver un système d'équations n'a pas trop été un problème, félicitations à ceux qui s'en sont sorti. A partir de ce système, un coup de résolution numérique permet de trouver les valeurs données par enigmatus.
On peut toutefois trouver les valeurs exactes. Le principe général de la résolution est le suivant : au lieu d'écrire les équations avec les rayons [latex]r_i[/latex], on les écrit avec [latex]x_i=\sqrt{r_i}[/latex].
Puis diverses substitutions permettent de se ramener à une équation de degré 4 à une inconnue, dont on peut extraire deux racines "simples" (pas besoin de méthode de Ferrari ou autre). Il reste alors une équation du second degré d'où on extrait la valeur [latex]x_i[/latex] recherchée.
Je posterai les détails dans quelques jours si personne n'a abouti d'ici-là.
#14 - 28-12-2017 17:27:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Sanagku
Bonjour à tous 
Ne te presse pas trop Ebichu , je n'ai eu aucun loisir pour chercher le problème et je pense avoir une approche légèrement différente de celles qui ont été proposées ( y compris la tienne ) .
A bientôt .
Vasimolo
#15 - 28-12-2017 17:56:53
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Sanaku
Alors je vais prendre mon temps  Je me demandais justement si on pouvait trouver une approche plus synthétique et moins analytique qui permette de simplifier la solution. Je me demandais justement si on pouvait trouver une approche plus synthétique et moins analytique qui permette de simplifier la solution.
#16 - 01-01-2018 12:36:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Sangaaku
J'ai fini par venir à bout du monstre 
Je donne les rayons des cercles en ordre croissant pour un carré de côté 4 :
[TeX]\ [/TeX]
[TeX]a=4-2\sqrt{3}[/TeX]
[TeX]b=9-5\sqrt{2}-5\sqrt{3}+3\sqrt{6} [/TeX]
[TeX]c=3-\sqrt{6}-\sqrt{2}+\sqrt{3}[/TeX]
[TeX]d=5-3\sqrt{2}-\sqrt{3}+\sqrt{6}[/TeX]
Je suis parti d'un petit cercle de rayon 4 en laissant libre le côté du carré , les calculs sont extrêmement fastidieux . J'attends la solution d'Ebichu ou une autre plus éclairante . D'un autre côté les problèmes du style sangaku sont souvent très calculatoires et la solution rarement miraculeuse . Mais bon , j'adore ces petits problèmes qui demandent beaucoup d'attention et de précision ( j'ai trop tendance à rêver et à me laisser distraire ) .
Excellente année à tous 
Vasimolo
#17 - 01-01-2018 18:18:27
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3838
sangzku
Pour le calcul, ce n'est pas du tout un petit problème, Vasimolo. J'ai laissé tomber à cause des erreurs d'écriture, de report....
En tout cas, le résultat est plus propre que je ne pensais, c'est même étonnant que ce soit si simple.
#18 - 02-01-2018 13:09:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Snagaku
Bravo Vasimolo ! Effectivement ça fait du bien, de temps en temps, des calculs bien bourrins...
Voici donc une solution détaillée.
Soient [latex]R_1<R_2<R_3<R_4[/latex] les rayons des 4 cercles. On obtient les relations suivantes (plusieurs personnes les ont observées, je ne reviens pas dessus) :
(1) [latex]R_3+R_4=2-\sqrt{2}[/latex]
(2) [latex]R_2+2\sqrt{R_2R_4}+R_4=1[/latex]
(3) [latex]R_2+2\sqrt{R_1R_2}+2\sqrt{R_1R_3}+R_3=1[/latex]
(4) [latex](R_2+2\sqrt{R_2R_4}-R_1)^2+(R_2+2\sqrt{R_1R_2}-R_4)^2=(R_1+R_4)^2[/latex]
On note alors a<b<c<d les racines carrées des rayons.
(2) donne [latex]b^2+2bd+d^2=1 \Leftrightarrow (b+d)^2=1 \Leftrightarrow b+d=1[/latex].
(4) donne [latex](b^2+2bd-a^2)^2+(b^2+2ab-d^2)^2=(a^2+d^2)^2[/latex] [latex]\Leftrightarrow (1-d^2-a^2)^2+(b^2+2ab-d^2)^2=(a^2+d^2)^2[/latex] [latex]\Leftrightarrow (b^2+2ab-d^2)^2=2(a^2+d^2)-1[/latex].
Résumons :
(1') [latex]c^2+d^2=2-\sqrt{2}[/latex]
(2') [latex]b+d=1[/latex]
(3') [latex]b^2+2ab+2ac+c^2=1[/latex]
(4') [latex](b^2+2ab-d^2)^2=2(a^2+d^2)-1[/latex]
On va alors, à l'aide de (1'), (2') et (4'), exprimer a, c et d en fonction de b. Puis on va reporter dans (3') pour avoir une équation à une seule inconnue, b.
(2') donne [latex]d=1-b[/latex]
(1') donne alors [latex]c=\sqrt{2-\sqrt{2}-(1-b)^2}[/latex]
Puis, dans (4'), on remplace d par (1-b), on développe, et il vient : [latex](2b^2-1)a^2+(4b^2-2b)a+b^2=0[/latex]. On résout cette équation du second degré en a, et on obtient [latex]a=\dfrac{b(2-\sqrt{2})}{\sqrt{2}-2b}[/latex].
Ainsi, en remplaçant a et c dans (3'), il vient l'équation suivante :
[TeX](8-4\sqrt{2})b^4+(-20+8\sqrt{2})b^3+(-6+12\sqrt{2})b^2+(-4\sqrt{2})b+1=0[/TeX]
Cette équation a le bon goût d'admettre deux racines "évidentes" (si vous avez de bons yeux, ou au moins une calculatrice graphique pour les observer sur la courbe) qui sont [latex]\frac{\sqrt{2}}{2}[/latex] et [latex]1-\frac{\sqrt{2}}{2}[/latex]. Malheureusement, aucune ne peut convenir pour b.
Donc on factorise l'équation en [latex](8-4\sqrt{2})(b-\frac{\sqrt{2}}{2})(b-1-\frac{\sqrt{2}}{2})[b^2+(-2+\frac{\sqrt{2}}{2})b+\frac{\sqrt{2}}{4}]=0[/latex]
Voici encore une équation du second degré à résoudre. La racine pertinente vaut : [latex]b=1-\frac{\sqrt{2}}{4}-\frac{\sqrt{3}}{2}+\frac{\sqrt{6}}{4}[/latex]
Il ne reste plus qu'à remonter cette valeur, et on obtient finalement :
[TeX]R_1=1-\frac{\sqrt{3}}{2}[/TeX]
[TeX]R_2=\frac{9-5\sqrt{2}-5\sqrt{3}+3\sqrt{6}}{4}[/TeX]
[TeX]R_3=\frac{3-\sqrt{2}+\sqrt{3}-\sqrt{6}}{4}[/TeX]
[TeX]R_4=\frac{5-3\sqrt{2}-\sqrt{3}+\sqrt{6}}{4}[/TeX]
#19 - 03-01-2018 17:59:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#20 - 03-01-2018 18:31:30
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
angaku
C'est un flash, ça m'a pris 10 secondes pour trouver le problème (et un peu plus pour le résoudre...). En fait je me suis dit : tiens, je vais faire un Sangaku. Bon, ben je vais mettre des cercles dans un carré, on va bien voir. J'en mets deux dans la diagonale, un troisième en haut à droite, et là je me dis : si je fais varier les tailles correctement, il doit y avoir moyen d'en faire rentrer un quatrième tangent à tout ce petit monde...
#21 - 03-01-2018 19:07:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
sangzku
C'est vraiment une belle intuition !!!
A priori rien ne laissait présager que la solution était unique .
On peut se demander ce qui se passe si on met quatre cercles sur deux côtés du carré ou encore trois cercles sur trois côtés ...
Mais c'est une autre histoire 
Bonne année à toi et à tous les P2T .
Vasimolo
#22 - 03-01-2018 20:51:05
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
dangaku
Bonne année à toi aussi !
Bientôt la galette, je connais quelqu'un qui va devoir reprendre du service... 
#23 - 03-01-2018 22:33:05
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3236
- Lieu: Luxembourg
|
 |

 Accueil
Accueil
 Forum
Forum








