 |
#1 - 20-04-2014 13:03:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 20-04-2014 14:12:59
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
gâteai 76
Euh ... ta boîte contient 45 oeufs. N'en voulais tu pas 40 ?
#3 - 20-04-2014 15:57:05
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
âGteau 76
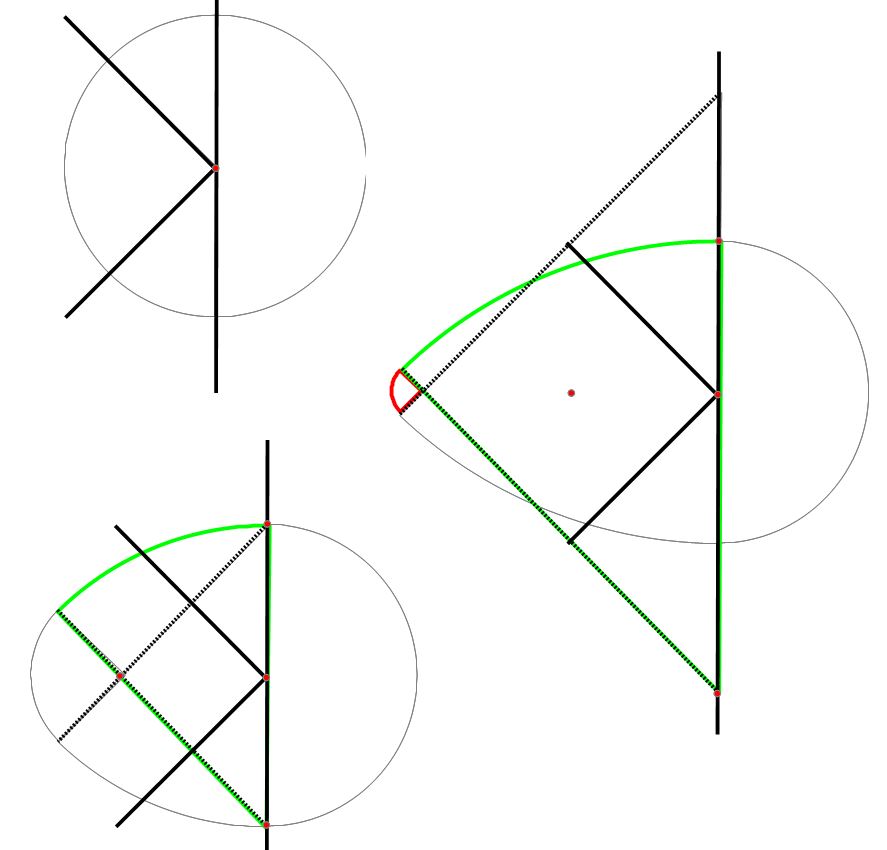
et la frontière de toute section contenant cet axe est constituée d'un demi cercle , un quart de cercle et deux huitièmes de cercle .
C'est vachement pas clair ! 
#4 - 20-04-2014 16:12:20
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
âteau 76
Je pense que c'est la forme du périmètre, à droite, il y a un demi-cercle, à gauche un quart de cercle, en haut et en bas, un huitième de cercle. Mais comment on peut calculer le volume, s'il n'y a pas de "hauteur" ? Parce que là, l'oeuf est plat ...
#5 - 20-04-2014 17:11:25
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
âGteau 76
@SabanSuresh: Dans la troisième dimension, l'œuf est circulaire. Je pense qu'il faut calculer son volume de révolution autour de son axe à l'aide d'une intégrale.
#6 - 20-04-2014 18:40:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 7
Une petite précision : la grille n'est qu'une illustration sur la façon de disposer les œufs , celle que va me fournir le pâtissier peut très bien contenir 42 œufs ( 7 X 6 ) ou autre . Le choix de la grille est imposé par la forme des œufs qui ne doivent être ni trop longs ni trop carrés : je vous laisse juges .
Bonne recherche 
Vasimolo
#7 - 21-04-2014 08:01:55
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteau 67
La disposition régulière demandée signifie que tous les œufs sont dans le même sens ? Ou faut-il aussi chercher une optimisation en autorisant les rotations ou les symétries ?
Edit : En commençant à réfléchir, je me suis demandé ce que tu entendais par régulier. Si il faut que les tangentes de chaque portion de cercle soit confondue à leurs jonctions, alors il ne peut pas s'agir de demi, quarts et 8èmes de cercle...
(la tangente avec le demi cerle est horizontale et celle avec le quart de cercle est à "45°", le 8ème de cercle ne peut pas récupérer 45° de différence...)
Du coup, faut-il comprendre que les rayons sont avec des rapports de 1, 1/2 et 1/4 en conservant ces tangentes confondues, ou faut-il oublier les tangentes et garder les demi, quart et huitièmes de cercle ?
#8 - 21-04-2014 10:32:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâreau 76
Pour répondre aux questions posées :
1°) Oui tous les œufs sont dans le même sens .
2°) Non , il n'y a pas de point anguleux ( une seule tangente aux points de jonction des arcs ) .
Vasimolo
#9 - 21-04-2014 21:35:19
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gteau 76
Bonjour 
je ne suis pas sûr de bien comprendre l'énoncé 
à mon avis la solution n'est pas unique.
Dans le cas dégénérer où l'on a des œufs sphériques on aurait 49 œufs de rayon 10/7 cm ce qui ferait un volume de :
[TeX]49 * {4\over 3}\pi * ({10\over 7})^3 = {4000\over 21}\pi \hbox{ cm}^3 = {4\over 21}\pi \hbox{ L}[/TeX]
Ce qui ferait une facture de
[latex]{4\over 21}\pi * 30 = {40\over 7}\pi\simeq 17,95[/latex] €
c'est un truc dans ce genre là qui est attendu ?
Il y a sûrement plus simple.
#10 - 21-04-2014 23:50:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gtâeau 76
Non Cogito , ce n'est pas tout à fait ce que j'attends 
Les œufs doivent avoir une forme d’œuf , ni trop ronds ni trop allongés .
Il me semble que la meilleure façon d'aborder l'énigme est d'essayer de dessiner un œuf et d'observer le rapport entre sa longueur et sa largeur . Ensuite il faudra regarder ce qui se passe pour un nombre d’œufs variant disons entre 40 et 50 .
Pour le moment on est très loin du début de l'approche d'une solution .
N’hésitez pas à poser des questions si le problème reste trop abscons .
Vasimolo
#11 - 22-04-2014 02:39:13
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
âGteau 76
On cherche bien une forme d’œuf qui soit composée d'un demi-cercle, d'un quart de cercle, et de deux huitième de cercles, telle que une quarantaine d’œufs de cette forme logent dans une boîte carrée de dimension 20cm * 20cm. Cette boite sera séparée en case, et chaque œuf devra être tangent aux bord de la case dans laquelle il sera placé. On supposera l'épaisseur des bord des cases de taille nuls.
Le découpage des cases sera du même genre que celui donné en exemple, c'est-à-dire que toutes les cases seront alignées et auront la même taille.
C'est bien cela ?
Il y a sûrement plus simple.
#12 - 22-04-2014 08:13:49
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Gâteu 76
Selon le centre choisi pour les 1/8 de cercle, ces oeufs auront des formes variables, non ? Alors pourquoi s'interroger sur le rapport largeur / longueur ?
#13 - 22-04-2014 09:55:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gââteau 76
@Cogito : c'est exactement ça .
@Gwen : l’œuf peut-il être deux fois plus long que large ?
Vasimolo
#14 - 22-04-2014 12:32:15
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
gâreau 76
Je pense que non, c'est limité par (2+rac(2)) fois le rayon du demi cercle
#15 - 22-04-2014 12:37:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtezu 76
Oui et ça devrait pas mal limiter les possibilités , il restera alors à choisir celle qui donne des œufs à têtes d’œufs 
Vasimolo
#16 - 22-04-2014 12:52:29
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
âteau 76
Je pense que la meilleure est celle qui double le rayon . On a donc des oeufs de rapport longueur/largeur de 1,53 environ contre 1,70 avec un oeuf version perforante.
#17 - 22-04-2014 16:14:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 7
Reste à voir ce que cela donne avec une bonne quarantaine d’œufs dans la boîte carrée .
Vasimolo
#18 - 22-04-2014 16:16:30
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
gâreau 76
Dans l'image ci-dessous, l'arc vert représente le quart de cercle, les arcs rouges représentent les huitième de cercle et l'arc bleu le demi-cercle.
[TeX]r[/latex] est le rayon du quart de cercle. Et je pose [latex]R[/latex], le rayon des huitièmes de cercle. Nous avons [latex]r \le R[/latex] (sinon l’œuf a une forme vraiment bizarre).
[latex]A[/latex] est le centre du quart de cercle.
[latex]B[/latex] et [latex]C[/latex] sont les centres des huitièmes de cercles.
[latex]J[/latex] est le centre du demi-cercle.
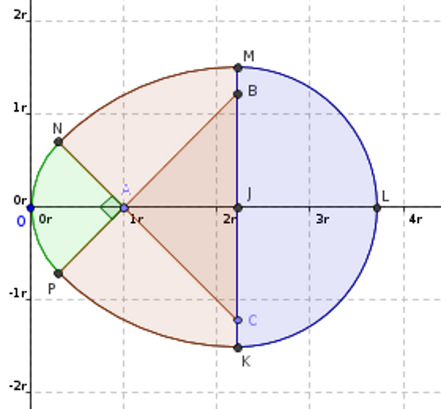
J'appelle [latex]x[/latex] la longueur [latex]OJ[/latex]. Nous avons [latex]r\le x[/latex].
Dans ce système de coordonnées, nous avons :
[latex]AN=AP=AO = r[/TeX][TeX]CM = CN = BK = BP = R[/TeX][TeX]JA=JB=JC = x-r[/TeX][TeX]A=(r,0) ; J=(x,0) ; C=(x,-(x-r)) ; B=(x,x-r);M=(x,R-(x-r))[/TeX][TeX]JM=JL=JK= R-(x-r)[/TeX]
Ce qui nous intéresse sont les longueurs [latex]OL[/latex] et [latex]MK[/latex].
Nous avons [latex]OL = OJ + JL = x + R - x + r = R + r[/latex].
Calculons [latex]MK[/latex] en fonction de [latex]r[/latex] et [latex]R[/latex].
Nous avons d'une part [latex]AC = CN - AN = R - r[/latex].
D'autre part [latex]AC=\sqrt{(x-r)^2 + (-(x-r))^2} = \sqrt{2}|x-r|=\sqrt{2}(x-r)[/latex]
Ceci nous donne que [latex]R-r = \sqrt{2}(x-r)[/latex] ce qui est équivalent à :
[TeX]\sqrt{2}(R-r) = 2(x-r)[/TeX]
Nous avons donc [latex]MK = JM + JK = 2R - 2(x-r) = 2R - \sqrt{2}(R-r) = (2-\sqrt{2})R + \sqrt{2}r[/latex].
Nous venons donc de calculer OL et MK, ce sont les dimensions de nos cases.
Maintenant on cherche des entiers [latex]m[/latex] et [latex]n[/latex] tels que :
i) [latex]m * OL = n * MK = 20[/latex]
ii) [latex]40\le m*n<50[/latex].
La condition i) nous dit que [latex]OL[/latex] et [latex]MK[/latex] doivent-être rationnels.
Recherchons des solutions dans [latex]\mathbb{Q}(\sqrt{2})[/latex] :
posons [latex]R = a\sqrt{2} + b[/latex] et [latex]r = c\sqrt{2} + d[/latex] avec [latex]a,b,c,d[/latex] rationnels.
-[latex]OL[/latex] rationnel nous dit que [latex]R + r = (a+c)\sqrt{2} + (b+d)[/latex] est rationnel et donc [latex]c=-a[/latex].
-[latex]MK[/latex] rationnel nous dit :
[TeX](2-\sqrt{2})R + \sqrt{2}r = (2-\sqrt{2})(a\sqrt{2} + b) + \sqrt{2}(-a\sqrt{2}+d)[/latex] est rationnel.
autrement dit :
[latex](2a - b + d)\sqrt{2} + (2b-4a)[/latex] est rationnel.
Nous avons donc la condition : [latex]2a = b - d[/latex] et donc [latex]2b - 4a =2d[/TeX]
Donc finalement on cherche deux rationnels [latex]b, d[/latex] et deux entiers [latex]m,n[/latex] tels que :
i) [latex]m * (b + d) = 20[/latex].
i')[latex] n * (2d) = 20 \leftrightarrow n*d = 10[/latex].
ii) [latex]40\le m*n<50[/latex].
J'appelle [latex]\rho[/latex] le rapport longueur/largeur, on a :
[TeX]\rho = OL/MK = (b+d)/(2d) = (20/m)/(20/n) = n/m[/TeX]
ii) nous dit que [latex]40/m^2 \le \rho < 50/m^2[/latex].
cas 1 : [latex]m = 1[/latex], donc : [latex]40\le \rho<50[/latex]
Le rapport longueur/largeur serait donc trop grand pour que les œufs aient une
tête d’œufs.
cas 2 : [latex]m = 2[/latex], donc : [latex]10\le\rho<12,5[/latex]
Le rapport longueur/largeur reste encore trop grand.
cas 3 : [latex]m = 3[/latex], donc : [latex]4,44..\le\rho<5,55..[/latex]
On va dire que c'est encore trop grand.
cas 4 : [latex]m = 4[/latex], donc : [latex]2,5\le\rho<3,125[/latex]
Je ne sais pas si c'est encore trop grand, mais je vais le supposer comme ça
j'aurai 3 cas en moins à étudier.
cas 5 : [latex]m = 5[/latex], donc : [latex]1,6\le\rho<2[/latex]
ça paraît pas mal.
* [latex]n=8; d=5/4; b = 11/4; \rho=1,6[/latex]
* [latex]n=9; d=10/9; b = 26/9; \rho=1,8[/latex]
cas 6 : [latex]m = 6[/latex], donc : [latex]1,11..\le\rho<1,3888[/latex]
On va dire que [latex]\rho=1,111[/latex] est trop proche de 1 donc l’œuf
sera trop rond. Par contre :
* [latex]n=8; d=5/4; b = 25/12; \rho=1,333[/latex] pourrait aller à la limite.
Pour les autres valeurs de [latex]m[/latex], on a un rapport trop petit pour avoir des beaux œufs.
Ce qui fait 3 solutions acceptables :
* [latex]m=5[/latex] et [latex]n = 8[/latex], alors [latex]d = 5/4[/latex] et [latex]b = 11/4[/latex] comme [latex]a = (b-d)/2[/latex]
on a [latex]a = 3/4[/latex] ce qui fait donc [latex]R={3\over 4}\sqrt{2} + {11\over 4}[/latex] et [latex]r = -{3\over 4}\sqrt{2}+{5\over 4}[/latex]
* [latex]m=5[/latex] et [latex]n = 9[/latex], alors [latex]d = 10/9[/latex] et [latex]b = 26/9[/latex] comme [latex]a = (b-d)/2[/latex]
on a [latex]a = 8/9[/latex] ce qui fait donc [latex]R={8\over 9}\sqrt{2} + {26\over 9}[/latex] et [latex]r = -{8\over 9}\sqrt{2}+{10\over 9}[/latex]
Ici nous avons un [latex]r < 0[/latex] donc cette solution est rejetée.
* [latex]m=6[/latex] et [latex]n = 8[/latex], alors [latex]d = 5/4[/latex] et [latex]b = 25/12[/latex] comme [latex]a = (b-d)/2[/latex]
on a [latex]a = 5/12[/latex] ce qui fait donc [latex]R={5\over 12}\sqrt{2} + {25\over 12}[/latex] et [latex]r = -{5\over 12}\sqrt{2}+{5\over 4}[/latex]
Bon et puis pour avoir une solution unique on va dire que en faite 1,33.. c'est pas un bon rapport. Donc finalement :
[TeX]m=5[/latex] et [latex]n = 8[/latex], [latex]R={3\over 4}\sqrt{2} + {11\over 4}[/latex] et [latex]r = -{3\over 4}\sqrt{2}+{5\over 4}[/TeX]
Ici je n'ai regardé que les solutions dans [latex]\mathbb{Q}(\sqrt{2})[/latex], je ne pense pas qu'il y ait des solutions ailleurs, mais si il y en a elle sont trop compliquée à chercher.
Maintenant calculer le volume de l’œuf c'est une autre affaire.
Voilà, j'espère ne pas avoir fait d'erreur de calculs.
Il y a sûrement plus simple.
#19 - 22-04-2014 19:40:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âGteau 76
Décidément tu aimes bien les calculs Cogito 
Voilà comment j'avais vu les choses : le rapport longueur largeur est aussi le rapport entre le nombre d’œufs disposés dans la longueur et dans la largeur . On essaie pour un nombre d'oeufs compris entre 40 et 50 :
40 :-> r=1,60
42 :-> r=1,17
45 :-> r=1,80
48 :-> r=1,33
49 :-> r=1,00
50 :-> r=1,00
Le bon rapport doit se situer entre 1,3 et 1,5 sinon l’œuf est trop carré ou trop pointu .

Sur le dessin [latex]a=\sqrt 2[/latex] et il faut diviser les mesures indiquées par 2,4 pour revenir aux données initiales .
Comme tu dis il reste à calculer le volume . Une formule qui peut aider , le volume du solide engendré par la rotation du domaine limité par le graphe d'une fonction f et l'axe des abscisses autour de cet axe : [latex]V=\pi\int_a^bf^2(x)dx[/latex] .
Vasimolo
#20 - 22-04-2014 20:18:05
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Gtâeau 76
Soit un œuf enfermé dans un parallélépipède AxBxB. Soient R1, R2 et R3 les rayons respectifs du quart, des deux huitièmes et du demi cercles et O1, O2 et O3 leurs centres respectifs.
On a les relations: A=(1–V2/2).R1+(V2/2).R2+R3 et: B=2.R3
Par ailleurs: O1O3=O2O3 donne: A=R1+R2
De plus: O1O2²=O1O3²+O2O3² donne: (R2–R1)²=(R2–R3)²+(A–R1–R3)²
d’où: (R2–R1)²=2.(R2–R3)², soit: R2²+2.R2.(R1–2.R3)+2.R3²-R1²=0
d’où: R2=(2+V2).R3–(1+V2).R1, et: A=-V2.R1+(1+V2/2).B
Finalement on a les expressions suivantes de R1, R2 et R3 en fonction de A et B:
R1=(-V2/2).A+(1/2+V2/2).B; R2=(1+V2/2).A-(1/2+V2/2).B et R3=B/2
Il me reste à calculer le volume par la somme de trois intégrales (et de voir comment optimiser ce volume en fonction de A et B), mais je reviendrai plus tard pour cela. J'ai fourni cette étape intermédiaire pour montrer que certains cherchent encore.
#21 - 23-04-2014 08:30:26
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâtteau 76
Comme moi aussi je suis un peu bizarre , j'ai demandé qu'il dispose régulièrement ses œufs dans une boîte carrée de 20 cm de côté :

Ça n'empêche pas de les mettre tête-bêche en 6 rangées de 7 soit 42
Chaque ligne aurait NRNRNRN (Normal/Reverse) et les séparations verticales du dessin ne sont plus vraies.
Cela ferait revoir les proportions longueur/largeur des œufs (hauteur = 20/6)
et assure un remplissage légèrement meilleur que NNNNNNN où le largueur vaut 20/7.
#22 - 23-04-2014 13:08:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtrau 76
L'objectif n'est pas de réaliser le meilleur taux de remplissage mais de poser les œufs dans des cases rectangulaires identiques . D'autre part je ne suis pas sûr qu'on puisse récupérer d'autres tailles de ces rectangles en acceptant un mélange de positions levées ou couchées . Il ne faut pas oublier que le rapport [latex]r=\frac Ll[/latex] est dans l'intervalle [latex][1;1+0,5\sqrt{2}][/latex] , on doit même réduire un peu l'intervalle si on veut une forme raisonnable .
Vasimolo
#23 - 23-04-2014 16:30:55
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteau 766
L'objectif n'est pas de réaliser le meilleur taux de remplissage mais de poser les œufs dans des cases rectangulaires identiques.
Si ça avait été dit dans l'énoncé...
#24 - 23-04-2014 19:41:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#25 - 23-04-2014 20:05:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteua 76
Mon pâtissier m'a présenté une facture de 15€ en me signifiant qu'il était bon prince 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










