Bonsoir,

Je veux bien croire qu'il est malin le bougre, mais quand même.

Choisissons deux pépites sur la boule de glace, et coupons la boule de glace
de façon à obtenir de demi-boules qui traversent chacune ces deux pépites.

Il reste trois pépites réparties sur ces deux demi-boules, donc il y a forcément une des deux demi-boules qui contient ou traverse deux de ces pépites (principe des tiroirs, ou des pigeons). Donc au moins une des deux demi-boules contient ou traverse au moins quatre pépites (les deux premières qui sont traversé par la coupe plus les deux "récupérées" du principe des tiroirs).

Donc à mon avis ton pâtissier bluff sur ce coup là !

Spoiler : [Afficher le message] Vous bluffez Martoni !

@Cogito : c'est tout bon
@Gwen : t'as rien de plus simple

Vasimolo

@Gwen : t'as rien de plus simple

Bah C'EST simple

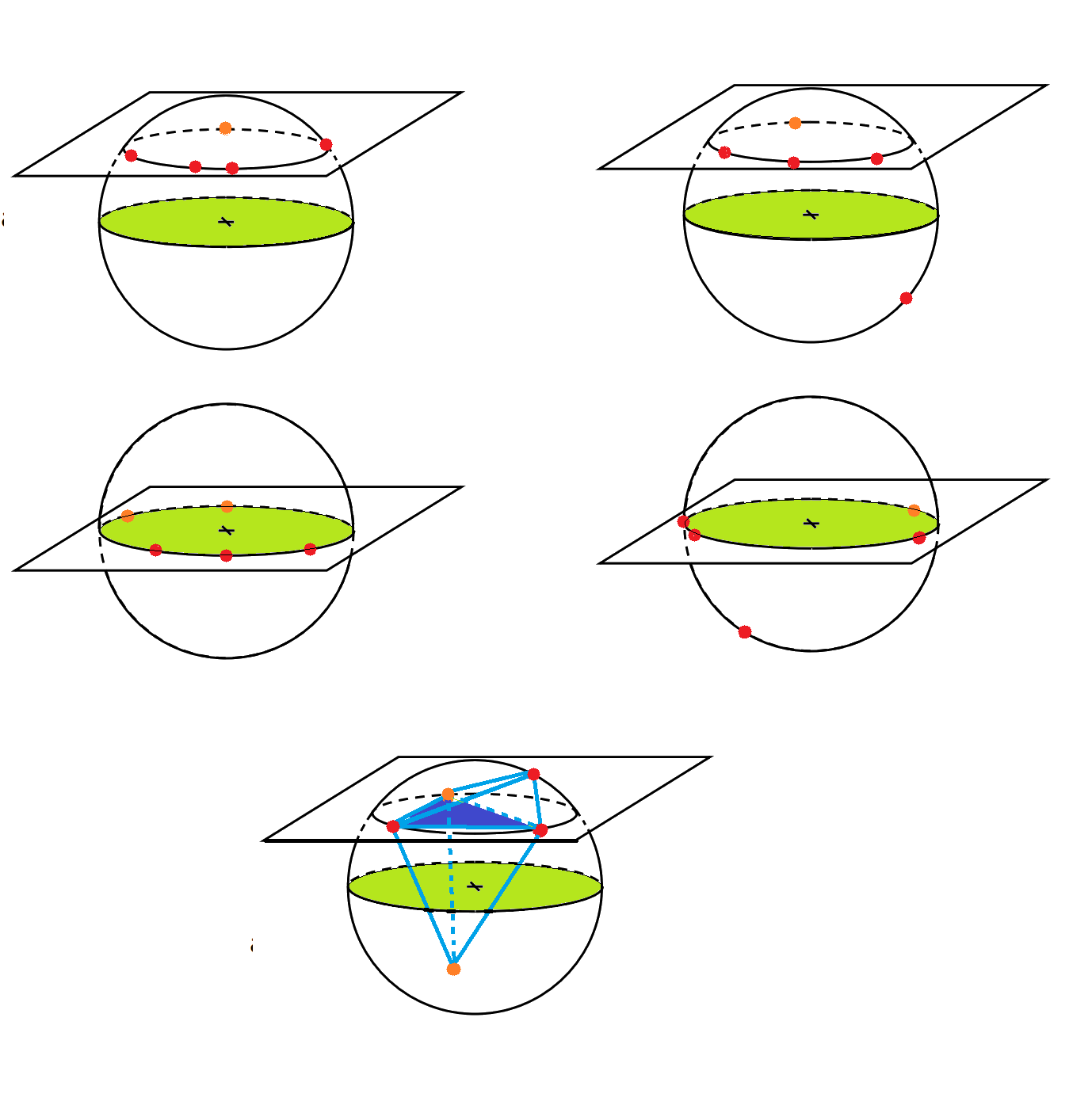
Cas 1 et 2 : 4 ou 5 points sont coplanaires. Je prends ce plan.
Cas 3 : Je prends 3 des points séparant le solide en deux pyramides ce qui définit un plan (bleu)

Dans tous les cas, le plan médian, parallèle au mien résout le problème.

Je dirais que le pâtissier a tort.
Il faut compter avec le 6 ème pt, centre de la boule, par où passe tout plan qui coupe la sphère en 2 moitiés égales. Tout plan qui passe par 2 des pts et le centre coupe la sphère en 2 demi sphères. Les 3 autres pts sont répartis ainsi: soit tous à l'extérieur du plan de coupe, alors il y en a forcément 2 d'un coté, et donc avec les 2 du plan, ça fait 4. Ou bien, il y en a 1 de ces 3 dans le plan de coupe, et donc au moins 1 dans l'une des demi sphères, ça fait encore 4. Si maintenant il y a au moins 4 pts dans le plan de coupe, ça fait encore 4.

Oui Nodgim , tu as la même solution que Cogito

Je conseille cette petite glace à ceux qui trouvent habituellement très lourdes voire indigestes les gourmandises de mon pâtissier .

La solution est garantie sans effort et plutôt agréable .

Vasimolo

C'est ça Dylasse

C'est vraiment tout bête , personnellement l'idée ne m'est pas venue tout de suite .

Vasimolo

J'oriente "correctement" la boule de glace. Puis, je projète orthogonalement les cinq pépites (situés sur la sphère) sur un cercle (de même diamètre). Enfin, je divise ce cercle en deux demi-cercles, de façon à ce que l'un d'entre eux contienne au moins quatre projections de pépites.
Ma "démonstration" est loin d'être rigoureuse, mais je dois probablement creuser cette idée de projection. Le "bon" choix de l'orientation de la sphère avant projection ET du trait de coupe du cercle final est évidemment primordial.

Vasimolo a écrit:

qu'une des moitiés contienne ou traverse au moins quatre des pépites .

J'avais compris qu'il était acceptable qu'une moitié contienne les 5 pépites,
sans contrainte sur la taille ni la position des pépites.
Le résultat est alors évident, le réponse est oui, c'est possible, il suffit de placer les 5 pépites sur une même hémisphère.
Enoncé pas clair.

Je suis un peu surpris de certaines réponses, quand on parle de 2 demi boules, alors la coupe passe par le centre de la boule non ? Aussi, dans le pire des cas, on ne peut au mieux que couper 2 pépites.
Il y a quelque chose que j'ai raté ?

C'est juste le msg 6 de Gwen, le mieux illustré. Il me semble qu'il coupe la sphère à des endroits non licites, ou alors j'ai mal lu.