 |
#1 - 14-03-2022 14:25:52
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Vous montez ? Non je descends ! [+ Indic]
Un petit problème à deux niveaux (je sais qu'un problème fortement similaire est déjà présent sur P2T depuis fort fort longtemps, mais bon... et puis le second niveau non  ) )
Donc, voilà, je suis dans un immeuble qui comporte n étages (plus le rez-de-chaussée). Cet immeuble dispose aussi de a ascenseurs.
Il y a un bouton unique pour appeler l'ascenseur. La règle qui s'applique à ce moment-là est :
1. L’ascenseur le plus près vient
2. En cas d'égalité, c'est un de ces ascenseurs les plus près, tous étant équiprobables
Je suis actuellement à l'étage e (avec 0≤e≤n).
Il n'y a pas d'ascenseur à mon étage : je l'appelle.
Première étape : Quelle est la probabilité (en fonction de n, e, a) que l'ascenseur arrive par en bas ?
Deuxième étape : Si vous avez répondu à la première étape de manière calculatoire, vous devriez arriver (après beaucoup de sueur) à un résultat étonnamment simple ! Et en général, quand un calcul de probabilité débouche sur un résultat aussi élégant, c'est qu'il y a une manière plus logique / moins calculatoire d'aborder le problème : laquelle ?
#2 - 15-03-2022 10:52:02
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Vous montez ? Non je descends ! [+ Idice]
Alors, bonne réponse pour 1 ascenseur 
Sans trop spoiler, on peut effectivement dire e/n 
A la question "avec un nombre d'ascenseur supérieur, cela changerait il quelque chose ?", prenons un exemple concret.
Je suis dans un immeuble de 10 étages, au 3ème
* Avec un seul ascenseur, s'il est au 0, 1 ou 2 c'est bon, de 4 à 10 non --> la probabilité qu'il arrive par en bas est de 30%
* Avec deux ascenseurs
* Arrivée par en bas 0-0, 0-1, 0-2, 0-7 à 0-10; 1-0, 1-1, 1-2, 1-6 à 1-10, 2-0, 2-1, 2-2, 2-5 à 2-10; 5-2; 6-1, 6-2; 7/8/9/10-0/1/2
* Arrivée par en bas avec un chance sur deux : 0-6, 1-5, 2-4, 6-0, 5-1, 4-2
Total : 42 possibilités sur les 100 possibles --> 42%
On voit donc bien que la probabilité est différente. Avec 3 ascenseurs, tu auras 46,8% etc...
en fait tu vas tendre vers 50% si le nombre d'ascenseur augmente (pour 10 ascenseurs, tu es à 49,99% environ)
#3 - 16-03-2022 09:31:59
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
vous montez ? non je descends ! [+ indicz]
Un indice pour démarrer : il faut calculer le nombre de combinaisons valides parmi les n^a combinaisons possibles.
La formule est la suivante :
Spoiler : [Afficher le message] Astuce : on se focalise sur les cas où e est dans la moitié basse. Pour la moitié haute, on peut tout à fait faire un système symétrique avec les ascenseurs qui arrivent par le haut 
Pour une distance D>0 la plus proche, on considère K>0 ascenseurs à cette distance, dont U≥0 par en bas, et on regarde combien ça fait de combinaisons. On somme tout ça pour tout 0≤U≤K, pour tout 1≤K≤a et pour tout 1≤D≤e
Somme(Nombre de combinaisons valides pour K ascenseurs à une distance de D, dont U ascenseurs à l’étage e-D, K-U à l’étage e+D, et a-K ascenseurs en dessous de e-D ou au dessus de e+D * U/K, pour D = 1..e, K = 1..a, U = 0..K)
Le U/K est pour l'équiprobabilité des ascenseurs ex-aequo en distance.
Après... y'a plus qu'à dérouler les calculs 
#4 - 21-03-2022 11:31:39
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
vous montez ? non jz descends ! [+ indice]
Allez, la solution "calculatoire" : comme indiqué plus haut, on se place pour e dans la première moitié de l'immeuble (et on fait le problème symétrique pour la partie haute); pour une distance D>0 la plus proche, on considère K>0 ascenseurs à cette distance, dont U≥0 par en bas, et on regarde combien ça fait de combinaisons. On somme tout ça pour tout 0≤U≤K, pour tout 1≤K≤a et pour tout 1≤D≤e
Somme(Nombre de combinaisons valides pour K ascenseurs à une distance de D, dont U ascenseurs à l’étage e-D, K-U à l’étage e+D, et a-K ascenseurs en dessous de e-D ou au dessus de e+D * U/K, pour D = 1..e, K = 1..a, U = 0..K)
Nombre de combinaisons valides =
[TeX]\sum_{D=1}^e\sum_{K=1}^a\sum_{U=0}^K{\frac{U}{K} * C_K^a * C_U^K * (n-2D)^{a-K}} = \\
\sum_{D=1}^e\sum_{K=1}^a{\left(C_K^a *(n-2D)^{a-K}*\sum_{U=0}^K{\frac{U}{K} * C_U^K }\right)} = \\
\sum_{D=1}^e\sum_{K=1}^a{\left(C_K^a *(n-2D)^{a-K}*\sum_{U=0}^K{\frac{U}{K} * \frac{K!}{U!(K-U)!}}\right)} = \\
\sum_{D=1}^e\sum_{K=1}^a{\left(C_K^a *(n-2D)^{a-K}*\sum_{U=0}^K{\frac{(K-1)!}{(U-1)!((K-1)-(U-1))!}}\right)} = \\
\sum_{D=1}^e\sum_{K=1}^a{\left(C_K^a *(n-2D)^{a-K}*\sum_{U=0}^K{C_{U-1}^{K-1}}\right)} = \\
\sum_{D=1}^e\sum_{K=1}^a{\left(C_K^a *(n-2D)^{a-K}*\sum_{U=-1}^{K-1}{C_U^{K-1}}\right)} = \\
\sum_{D=1}^e\sum_{K=1}^a{\left(C_K^a *(n-2D)^{a-K}*2^{K-1}\right)} = \\
\frac{1}{2}\sum_{D=1}^e\left(\sum_{K=1}^a{\left(C_K^a *(n-2D)^{a-K}*2^K\right)}\right) = \\
\frac{1}{2}\sum_{D=1}^e\left(\sum_{K=0}^a{\left(C_K^a *(n-2D)^{a-K}*2^K\right)}-(n-2D)^a\right) = \\
\frac{1}{2}\sum_{D=1}^e\left((n-2D+2)^a-(n-2D)^a\right) = \\
\frac{1}{2}\left(\sum_{D=1}^e(n-2D+2)^a-\sum_{D=1}^e(n-2D)^a\right) = \\
\frac{1}{2}\left(\sum_{D=0}^{e-1}(n-2D)^a-\sum_{D=1}^e(n-2D)^a\right) = \\
\frac{1}{2}\left(n^a-(n-2e)^a\right)
[/TeX]
Et donc, on arrive à la formule, à la fois simple et élégante :
[TeX]\frac{n^a-(n-2e)^a}{2n^a}[/TeX]
Et comme je l'indiquais au tout début, quand c'est aussi élégant, il y a surement une autre manière d'arriver au résultat 
Maintenant à vous de jouer
#5 - 17-07-2022 09:59:43
- LeJeu
- Passionné de Prise2Tete
- Enigmes résolues : 25
- Messages : 92
vous montez ? non je dzscends ! [+ indice]
Il me semble que ce fil est toujours ouvert , Scarta 'vient' de donner :
[TeX]P_M(e,n,a)=\frac{n^a-(n-2e)^a}{2n^a}[/TeX] ( Probabilité qu'un ascenceur d'une série de a ascenseurs arrive en montant à l'étage e, avec e en partie basse d'un immeuble allant de 0 à n étages)
C'est à dire : [TeX]P_M(e,n,a)=\frac{1}{2} - \frac{1}{2}(1-2 \frac{e}{n})^a[/TeX]
( qui montre bien la convergence vers 1/2)
Reprenons l'exemple de n=10 , e= 3 , a= 2 : et calculons plutôt la probabilité qu'un ascenseur arrive en descendant :
1 cas) : Les deux ascenseurs A et B arrivent par le haut Proba=7/10 *7/10
2 cas) : Un arrive par le bas , l'autre par le haut
supposons que A arrive par le bas ( donc de l'un des trois étages), pour qu'il y ait match avec B qui arrive du haut, il faut aussi que B arrive d'un des trois étages au dessus de e , et alors B aura une chance sur deux de gagner; ce qui nous donne Proba = 1/2* 3/10*3/10
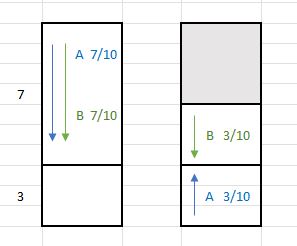
ce qui nous donne en inversant A et B dans le cas 2:
P = 7/10*7/10 + 2 ( 1/2*3/10*3/10) = 58 % , on retrouve bien la probabilité précédente de montée de 42 %
la formule pour deux ascenseurs :
[TeX] P_D(2) = (\frac{n-e}{n})^2 +(\frac{e}{n})^2[/TeX]
ce qui donne
[TeX]P_D(e,n,2)=\frac{1}{2} + \frac{1}{2}(1-2 \frac{e}{n})^2[/TeX]
La suite se fait par récurrence on suppose vraie P(a) et on calcul P(a+1)
on scinde en deux : les 'a ' ascenseurs et le "a+1" ieme
1 cas) un des 'a' ascenseurs arrive par le haut et le (a+1)ième aussi
proba = P(a) * ( 1-e/n)
2 cas ) un des 'a' ascenseurs arrive par le bas et le (a+1) ieme par le haut
comme dans notre exemple précédent pour qu'il ait match, il faut que l’ascenseur (a+1) arrivent des e étages au dessus de e et
proba = 1/2 * ( 1-P(a)) * e/n
3 cas) un des 'a' ascenceur arrive par le haut mais des e étages au dessus de e, et l'ascenceur a+1 arrive du bas
la proba d'arrivée du haut des e premiers étages au dessus de e = proba d'arrivée du bas des e étages en dessous de e
on a proba = 1/2 * ( 1-P(a)) * e/n
au final [TeX]P_D(a+1) = P_D(a) * ( 1-\frac{e}{n}) + ( 1-P_D(a)) *\frac{e}{n}[/TeX]
ce qui se simplifie en [TeX]P_D(a+1) = P_D(a) * ( 1-\frac{2e}{n}) + \frac{e}{n}[/TeX]
et donc [TeX]P_D(e,n,a+1)=\frac{1}{2} + \frac{1}{2}(1-2 \frac{e}{n})^{(a+1)}[/TeX]
ce qui valide bien la formule :
[TeX]P_D(e,n,a)=\frac{1}{2} + \frac{1}{2}(1-2 \frac{e}{n})^{a}[/TeX]
et donc celle pour la montée calculée ( je n'ai pas réussi à suivre le calcul...) par Scarta
[TeX]P_M(e,n,a)=\frac{1}{2} - \frac{1}{2}(1-2 \frac{e}{n})^{a}[/TeX]
#6 - 18-07-2022 10:44:00
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Vous montez ? Non je descend s! [+ Indice]
Oula... même moi je me rappelle plus ce qu'il fallait dire 
De mémoire : ça correspond tout simplement à la probabilité de
1. ne pas avoir tous les ascenseurs a-delà de 2e de distance (sinon ils viennent tous par en haut !)
2. et pour les autres cas : c'est tout simplement une chance sur deux EN MOYENNE. Chaque cas est compensé par un cas symétrique.
Par exemple je suis au 3ème, il y a un ascenseur au 2nd, un au 1er et un au 5ème, la probabilité sera la symétrique du cas ou j'ai un ascenseur au 4ème, un au 5ème et un au 1er (symétrique par rapport à moi). Dans le premier cas la probabilité d'arriver par en bas est de 1, dans l'autre cas elle est de 0 --> moyenne de 1/2
Autre exemple : je suis au 5ème, il y a deux ascenseurs au 4ème, un au 6ème et un au 7ème --> symétrique de "deux au 6ème, un au 4ème et un au 3ème".
Premier cas : probabilité de 2/3, second cas : probabilité de 1/3 --> moyenne de 1/2
Si on exclu tous les cas où les ascenseurs sont tous au delà de 2e de distance, c'est parce qu'ils n'ont pas de symétriques !
(et pour les cas où quelques ascenseurs mais pas tous seraient au delà de 2e... on ne regarde pas ces ascenseurs tout simplement - ils ne change pas le calcul)
D'où la formule : "un demi" x "nombre de combinaisons avec au moins un ascenseur à une distance de 2e max" / "nombre total de combinaisons"
Et comme "nombre de combinaisons avec au moins un ascenseur à une distance de 2e max" vaut "nombre total" - "nombre de combinaisons avec tous les ascenseurs à sur les (n-2e) autres étages"
... on obtient :
[TeX]\frac{1}{2}\frac{n^a - (n-2e)^a}{n^a}=\frac{n^a - (n-2e)^a}{2n^a}[/TeX]
|
 |

 Accueil
Accueil
 Forum
Forum







