|
#1 - 16-07-2024 22:12:14
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
#2 - 17-07-2024 07:23:01
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 894
- Lieu: Ville 2/N près 2*i
Devoir de vcances...
Salut JackV,
Je ne sais pas si j'ai bien compris l'énoncé. le but est d'avoir un maximum de faces non superposables ?
Dans ce cas, dès n=3, je peux obtenir 6 faces non-superposables.
Désolé pour l'aspect un peu applati du carré ci dessous :-p
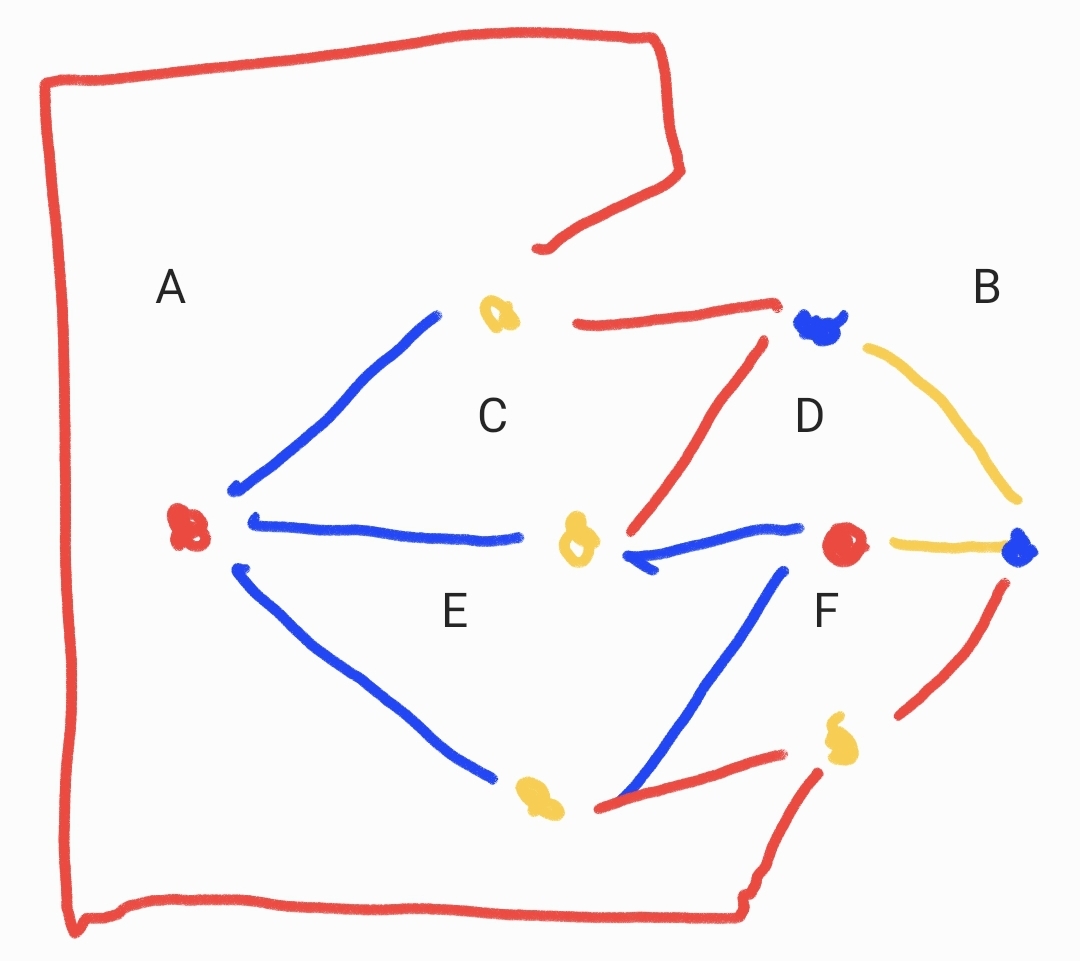
Verification de la superposabilité. je suis parti du principe que les faces sont des objets mathématiques sans épaisseur. Conséquence, on peut "retourner la face" pour la superposer. Autre façon de voir les choses, le reflet dans le miroir est toujours superperposable à l'original.
Pour faciliter la vérification, j'introduis une nomenclature RJB des faces.
RJB pour la couleur des arêtes parcourues dans l'ordre, rjb pour les sommets rencontrés.
On garantit l'unicité de la description en choisissant le point de départ et le sens de parcours qui maximisent les nombre de R en début de chaîne, puis le nombre de J, puis si braiment il le faut, le nombre de B, de r, de j, de b.
Deux faces sont alors superposables ssi leur descriptions sont égales.
Notre carré donne :
A=RjRjBrBj (palindrome)
B=RjRjRbJb (palindrome)
C=RbRjBrBj (palindrome)
D=RbJbJrBj (chiral)
E=BrBjBrBj (palindrome)
F=RjRbJrBj (chiral)
On a bien 6 faces non superposables.
#3 - 17-07-2024 09:27:34
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
drvoir de vacances...
Merci Migou pour ta contribution  . .
Quand je parlais de "non superposables", je pensais simplement "par rotation", et non "en miroir".
#4 - 17-07-2024 12:48:49
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 894
- Lieu: Ville 2/N près 2*i
Devoir de vacances..
Ok, et du coup, avec la superposition sans retournement/miroir ma figure marche aussi.
On a bien 6 faces distinctes dès n=3.
Ensuite pour le (2), le but est d'avoir au plus 2 éléments parmi 8 qui ont la même couleur ?
#5 - 17-07-2024 17:10:51
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Dveoir de vacances...
Migou a écrit:pour le (2), le but est d'avoir au plus 2 éléments parmi 8 qui ont la même couleur ?
Exact  , et c'est valable pour n > 3. , et c'est valable pour n > 3.
#6 - 18-07-2024 17:30:11
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 894
- Lieu: Ville 2/N près 2*i
Devoir de vaacnces...
OK, maintenant que j'ai relu ca me parait clair.
(en fait, je ne sais pas pourquoi, j'imaginais n>=7 avec une seule répétition parmis les 8)
#7 - 18-07-2024 18:27:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Devoir de vacanes...
Je ne comprends pas grand chose 
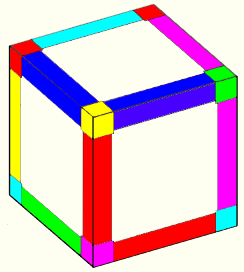
Sur l'illustration chaque cube d'angle est monochrome et tous les cubes entre deux coins sont aussi monochromes . Un cube de coin ne doit pas être en contact avec un cube de même couleur . Est-ce la situation et surtout quelle est la la question 
Vasimolo
#8 - 18-07-2024 19:45:53
- Spirou
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 501
Devoir de vacannces...
Je tente une idée:
(1) Nous pouvons nommer [latex]E[/latex] le sous ensemble de[latex] [|1,n|]^8[/latex] tel que [latex](a_1,\dots , a_8) \in E[/latex] si et seulement si [latex]
a_i \neq a_{i+1}
[/latex] pour tout [latex]i[/latex] (avec la convention [latex]a_9=a_1[/latex]).
Alors [latex]\mathbb{Z} / 4\mathbb{Z}[/latex] agit sur [latex]E[/latex], et on cherche le nombre d'orbites.
Le fixateur de [latex]\overline{1}[/latex] ainsi que celui de [latex]\overline{3}[/latex] sont de cardinal [latex]n(n-1)[/latex].
Celui de [latex]\overline{2}[/latex] est de [latex]n(n-1)^2 + n(n-1)(n-2)^2[/latex].
D'après la formule de Burnside, le nombre total d'orbites est donc égal à
[TeX]
\[
\frac{n(n-1)(n+1) + n(n-1)(n-2)^2 + \text{Card}(E)}{4}
\]
[/TeX]
Pour le cardinal de [latex]E[/latex] je ne suis pas sur, j'ai trouvé [latex]n(n-1)^7 - n((n-1)(n-2)^5 + 4(n-1)^2(n-2)^3 + 3(n-1)^3(n-2))[/latex]
mais c'est à vérifier!
Pour les premières valeurs j'obtiens alors:
2 pour [latex]n=2[/latex]
72 pour [latex]n = 3[/latex]
1668 pour [latex]n = 4[/latex]
Pour le (2), est-ce c'est une seule couleur qui a le droit d'apparaitre deux fois? Par exemple, est-ce qu'une face avec deux arêtes rouges et deux arêtes bleues est autorisée? Ou est-ce que toutes les zones doivent être de couleurs différentes, à l'exception de éventuellement deux zones? (Dans ce cas, il faudrait au moins 7 couleurs pour peindre une face)
#9 - 18-07-2024 22:04:01
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Devoir de vvacances...
A Vasimolo : l'illustration me parait assez claire : chaque coin du cube est bien sûr d'un seule couleur, qui apparaît sur les trois faces concernées par ce coin. et chaque arête est d'une seule couleur partagée par les deux faces concernées.
A Spirou : pour le 1), ta proposition me parait bien complexe, mais je ne saurais la juger (tu es certainement bien meilleur mathématicien que moi...)
Pour ta question sur le 2), je reconnais que ma formulation était très ambigüe. J'ai modifié le sujet en conséquence.
Pour comparer les solutions proposées qui peuvent prendre des formes très différentes, pourriez-vous SVP donner des valeurs chiffrées pour n = 3 et n = 4 ?
#10 - 19-07-2024 14:20:16
- Spirou
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 501
Devoir de vacances..
J'ai corrigé le (1) et donné des valeurs numériques pour les premiers cas.
Pour le (2), je commence par compter le nombre de facon de colorier une face, sans prendre en compte les redondances dues aux rotations.
Si toutes les zones sont de couleurs distinctes, j'ai [latex]n(n-1)\dots (n-7)[/latex] choix.
Si il y a exactement une paire d'une meme couleur, j'ai [latex]20n(n-1)\dots (n-6)[/latex] choix.
Si il y a exactement deux paires de la même couleur, j'en ai [latex]110n(n-1)\dots (n-5)[/latex].
Pour trois paires, cela m'en fait [latex]164n(n-1)\dots (n-4)[/latex].
Enfin, quatre paires m'en donnent [latex]31n(n-1)(n-2)(n-3)[/latex].
A ce nombre je rajoute le fixateur de [latex]\overline{2}[/latex] qui est de cardinal [latex]n(n-1)(n-2)(n-3)[/latex].
Et je divise par 4, l'order du groupe qui agit.
J'obtiens en conséquence la formule
[TeX]\[
\frac{n^8 - 8 n^7 + 12 n^6 + 54 n^5 - 189 n^4 + 146 n^3 + 80 n^2 - 96 n
}{4}
\][/TeX]
qui me donne pour [latex]n=4[/latex] la valeur 192
et pour [latex]n=5[/latex] la valeur 5880.
#11 - 19-07-2024 19:29:51
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Deovir de vacances...
Merci Spirou  pour ton post bien détaillé et surtout pour avoir bien respecté ma demande au sujet des valeurs numériques. Je ne me sens pas capable de juger tous tes résultats, mais j'espère que d'autres spécialistes de ton acabit viendront confirmer tes réponses pour ton post bien détaillé et surtout pour avoir bien respecté ma demande au sujet des valeurs numériques. Je ne me sens pas capable de juger tous tes résultats, mais j'espère que d'autres spécialistes de ton acabit viendront confirmer tes réponses  . .
#12 - 23-07-2024 08:57:00
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3612
- Lieu: 94110
Devor de vacances...
Merci aux participants  , spécialement pour Spirou qui s'est fortement impliqué. , spécialement pour Spirou qui s'est fortement impliqué.
Pour les questions 1 et 2, ses résultats rejoignent les miens pour les cas hyper-simples.
Je laisse le soin aux matheux de vérifier ses généralisations.
|
 |

 Accueil
Accueil
 Forum
Forum