 |
#1 - 09-03-2025 13:39:24
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1426
- Lieu: Nicastro / Tronville
jeu des truangles (déplacé)
(question ouverte)
Ce jeu se joue sur une feuille quadrillée
On marque par une croix n rangées de n points (les intersections de lignes
(à l'intérieur d'un carré de (n+1) X (n+1)
Par exemple ici 8 X 8

Chaque joueur trace à son tour un triangle joignant trois points non déjà utilisés, sans couper des segments déjà tracés
Celui qui ne peut plus continuer a perdu.
La question posée est qui a une stratégie gagnante pour
4 points
9 points
16 points
25 points
Y a-t-il une règle pour n ? (par exemple dépendant de la parité)
Lélio Lacaille - Du fagot des Nombreux
#2 - 09-03-2025 23:30:57
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 896
- Lieu: Ville 2/N près 2*i
jeu des trizngles (déplacé)
Pour 4 et 9, il est possible de bloquer totalement le jeu en un coup.
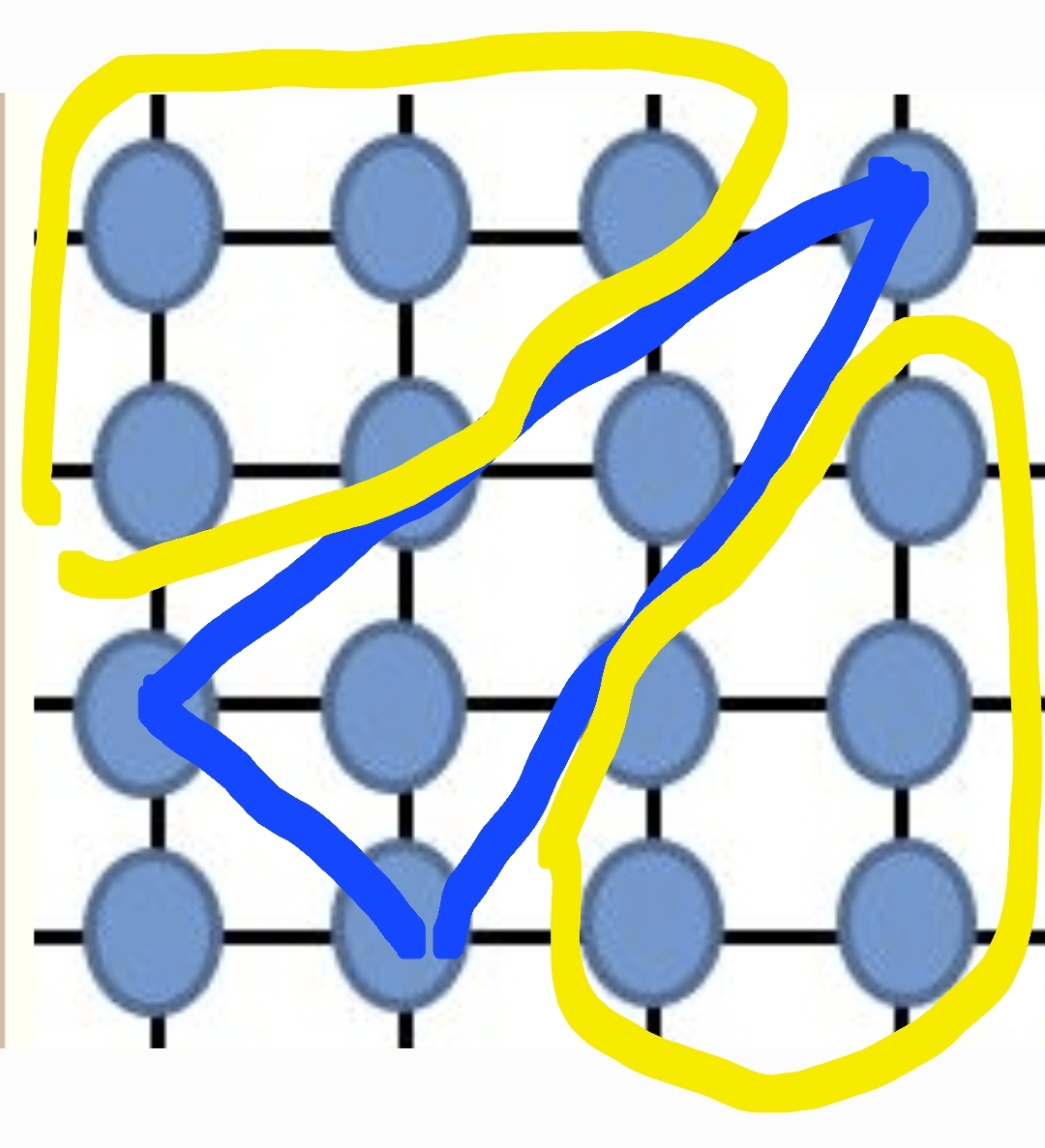
pour 16, on peut délimiter le terrain en deux triangles en jouannt le triangle bleu. Il reste 5 cases de part et d'autre, ce qui interdit de faire plus d'un triangle par zone.
#3 - 10-03-2025 08:52:34
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 896
- Lieu: Ville 2/N près 2*i
Jeu des triangles (déplac)
petite demande de précision sur le jeu.
Et-ce u'on est d'accord sr les trois regles suivantes ?
1) les triangles dégénérés (applatis) sont interdits
2) on peut dessiner un triangle dans un triangle deja dessiné.
3) un point est pris seulement si la ligne passe exactement dessus. par exemple, si je trace un trait formant le vecteur (+2, +4), je vais prendre au passage le point intermédiaire (+1, +2)
par contre, si j'opte pour un trait (+1,+5) par exemple, je vais frôler un certain nombre de points mais tous resteront libres.
#4 - 10-03-2025 14:59:17
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1426
- Lieu: Nicastro / Tronville
jeu ded triangles (déplacé)
@migou a écrit
petite demande de précision sur le jeu.
Et-ce u'on est d'accord sr les trois regles suivantes ?
1) les triangles dégénérés (applatis) sont interdits
2) on peut dessiner un triangle dans un triangle deja dessiné.
3) un point est pris seulement si la ligne passe exactement dessus. par exemple, si je trace un trait formant le vecteur (+2, +4), je vais prendre au passage le point intermédiaire (+1, +2)
par contre, si j'opte pour un trait (+1,+5) par exemple, je vais frôler un certain nombre de points mais tous resteront libres.
Je me permets de recopier ici du fait de l'utilité de sa question
Et la réponse est oui pour tout
Merci @migou pour ta demande de précision
Lélio Lacaille - Du fagot des Nombreux
#5 - 11-03-2025 15:27:23
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 896
- Lieu: Ville 2/N près 2*i
jei des triangles (déplacé)
Une stratégie gagnante consiste à toujours laisser à l'adversaire des couples de zones aux mêmes caractéristiques, par exemple : deux zones pouvant contenir 1 triangle mais pas plus ; et deux autres zones pouvant contenir de 1 à 3 triangles.
De cette façon, à chaque coup de l'adversaire on joue un coup symétrique, jusqu'à la victoire.
C'est assez facile pour les carrés 16 et 25, en revanche je peine à appliquer cette stratégie au carré de 36.
...
Bigre ! C'est quasiment en l'écrivant que ça m'est venu !
Je crois bien que j'ai la solution pour toutes tailles !
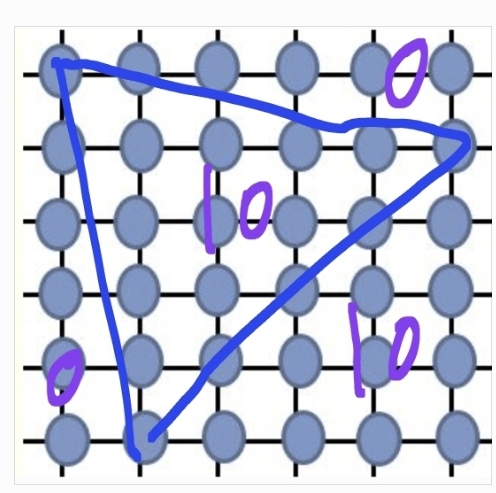
quel que soit la taille c du coté du carré, en reliant les points (0,0) (c-1,1) et (1,c-1), je délimite deux zones mortes sur les côtés et deux zones symétriques : une dans le triangle et l'autre à l'extérieur.
A partir de là, je gagne en jouant le symétrique du coup de l'adversaire.
#6 - 12-03-2025 18:51:52
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
jei des triangles (déplacé)
Salut Aunryz.
Après le jeu de Nim avec les nombres premiers....
Ma réponse est : toujours gagnant !
Si l'on place les n² points dans le repère orthonormé, celui en bas à gauche correspondant à (x;y)= (0;0) , alors :
Il suffit de jouer le triangle ( n-2;0) (0;n-2) (n-1;n-1) qui partage le carré en 2 zones identiques exploitables. Il suffit alors au 1er joueur de jouer en miroir le jeu du 2ème joueur !
Jolie énigme !
#7 - 13-03-2025 01:38:03
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1426
- Lieu: Nicastro / Tronville
jei des triangles (déplacé)
Pour Migou comme pour Nodgim
Il me semble que l'adversaire peut jouer un coup symétrique
(mais je bourde facilement)
Par rapport à [(0;0) ; (n;n)] pour Migou
Par rapport à [(0;n) ; (n;0)] pour Nodgim
Un triangle qui empêche l'adversaire de produire un symétrique serait
par exemple le triangle (0;0) (0;n) (n;0)
Mais la suite me parait incertaine au-delà de n=8
?
Lélio Lacaille - Du fagot des Nombreux
#8 - 13-03-2025 06:47:21
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Jeu des triangles (éplacé)
@ Aunryz : c'est le 1er joueur qui place le triangle tel qu'indiqué, la symétrie des 2 zones exploitables, en forme de triangle rectangle d'égales dimensions est évidente.
Pour clarifier les idées, je donne ici un carré de 7*7 points, les trois 1 étant choisis pour le triangle initial :
0 0 0 0 0 0 1
1 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 1 0
#9 - 13-03-2025 17:50:22
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
jeu des triangles (séplacé)
Bonjour, je pense que déjà, toute grille est gagnante pour le premier joueur.
Il est possible de la "partager en 2" selon son axe central en diagonale avec un triangle n'admettant ni triangle intérieur, ni contournement.
A tout coup joué par le second joueur, le premier pourra répondre par un tracé symétrique, avec l'assurance de gagner.
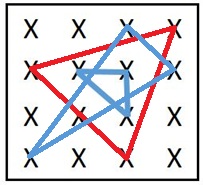
Un exemple de ce tracé pour une grille 7x7 :
#10 - 13-03-2025 19:52:29
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1426
- Lieu: Nicastro / Tronville
Jeu des rtiangles (déplacé)
Je viens de comprendre !
Vous avez parfaitement raison avec cette vieille version de mon jeu que j'ai recopié par inadvertance
Qui est l'énoncé de cette énigme que vous avez utilisée.
Et donc, oui ... c'est la conclusion à laquelle nous étions arrivé avec l'ami en compagnie duquel j'avais inventé (mais certainement d'autres en même temps que moi) ce petit jeu.
Le premier qui joue gagne par la stratégie que vous avez tous les trois développés.
La version un peu plus complexe de ce jeu est celle qui permet aux segments de ce croiser, un point traversé étant considéré comme pris et donc ne pouvant être ni un nouveau sommet ni un point d'un nouveau segment.
Si vous en êtes d'accord, pour laisser ce fil cohérent.
lorsque son temps sera écoulé j'ouvrirai un autre sujet avec cette règle là.
(à moins que vous préfériez continuer sur ce fil avec la nouvelle règle)
Merci de votre participation fructueuse Migou nodgim et Gwen
Lélio Lacaille - Du fagot des Nombreux
#11 - 13-03-2025 20:44:41
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
heu des triangles (déplacé)
Ca sent l'arnaque ce truc-là...
Tu as voulu créer une question ouverte, et elle ne l'est pas.
Je ne pense pas que par inadvertance on puisse autoriser ou refuser des croisements de chemins.
#12 - 15-03-2025 09:26:09
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 896
- Lieu: Ville 2/N près 2*i
Jeu des triangless (déplacé)
Personnellement j'aimerais bien l'autre version du jeu, et sur un fil séparé. Mais je n'ai pas l'impression qu'il y ait une stratégie claire.
#13 - 15-03-2025 19:11:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Jeu des trriangles (déplacé)
La stratégie est classique , on partage le jeu en deux et on joue en miroir , le plus difficile est de dénicher le triangle initial qui fournit la bonne partition . Je ne vois pas trop l'intérêt d'autoriser les croisements mais construire de carrés à la place des triangles peut offrir d'autres perspectives .
Vasimolo
#14 - 15-03-2025 20:15:17
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1426
- Lieu: Nicastro / Tronville
Jeu dess triangles (déplacé)
gwen27 a écrit:Ca sent l'arnaque ce truc-là...
Tu as voulu créer une question ouverte, et elle ne l'est pas.
Je ne pense pas que par inadvertance on puisse autoriser ou refuser des croisements de chemins.
Je pense que tu as déjà fait Gwen un copié collé. Parfois on ne vérifie pas suffisamment le contenu de la phrase, notamment lorsqu'il est proche de celui qu'on voulait réellement recopier.
J'ai des milliers de documents sur deux ordinateurs (identiques, mais dédiés à des travaux différents) , une dizaines de disques durs, externes, quelques piles de cd, et à 70ans dans l'année, il m'arrive de plus en plus d'être distrait.
Crois en ma bonne foi, je t'en remercierais.
Si tu reprends les réponses que j'ai faites à Migou et Nodgim
Par rapport à [(0;0) ; (n;n)] pour Migou
Par rapport à [(0;n) ; (n;0)] pour Nodgim
tu verras que celles-ci supposent l'intersection possible.
Encore une fois, je suis désolé, de cette étourderie.
Disons qu'elle nous a permis, pour peu que la version complexe soit intéressante à cerner, une entrée en matière.
Merci à vous Migou Gwen et Nodgim pour votre participation
et peut-être à bientôt sur la version croisements autorisés.
Lélio Lacaille - Du fagot des Nombreux
|
 |

 Accueil
Accueil
 Forum
Forum










