Chouette une nouvelle proposition.
1- Je suis certainement dans l'erreur ? Mais j'ai l'impression qu'il n'y a pas un chemin plus court (mais deux) pour contourner la table, la figure d'ensemble me paraissant symétrique
2- Si je ne tiens pas compte du 1
il me semble que si la personne contourne la table, tous les points de sa personne ne font pas le même chemin. Je suis donc embêté pour répondre à la question. A moins que l'on considère le point de sa personne qui fait le trajet le plus court, mais alors ...
3 - la carrure de la personne (sa largeur) me semble être un paramètre important de ce contournement. Il me semble qu'on ne peut donc pas donner une réponse absolue.
Faut-il donner une réponse paramétrée dans laquelle se trouverait x largeur de la personne.
REM : dans ce cas le problème est plus compliqué
Il faut déterminer quel est le point (ici du petit cercle)
qui va passer tangentiellement le grand cercle
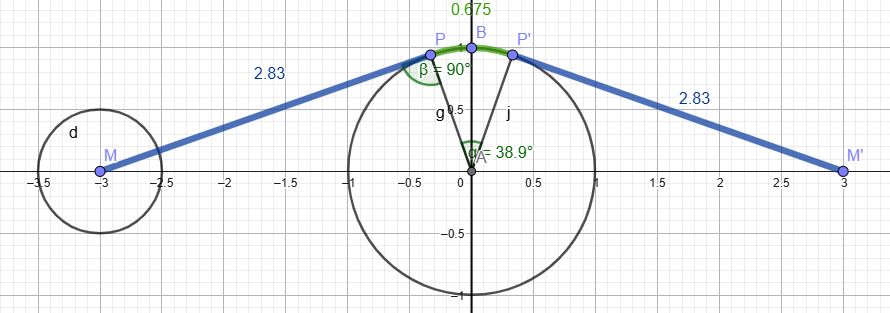
4 - si j'adopte les conventions implicites des mathématiques qui réduisent la réalité à des points (isolés ou ensembles de points)
et que je considère que la personne est sans dimension et est assimilable au point M(-3,0) ( l'arrivée étant M'(3,0) )
Alors le trajet pour contourner la table est composé de trois parties,
un segment de droite, tangent au cercle au point M'
un arc de cercle (de la table) qui joint le point P au point P' symétrique de P' par rapport à la médiatrice de [MM'] et le segment [P'M'] symétrique de [PM] par rapport à la médiatrice de [MM']
Il reste à déterminer la longueur MP et (pour déterminer la longueur de l'arc PP')
la mesure de l'angle.
Le segment tangent est le grand côté de l'angle droit d'un triangle rectangle d'Hypoténus 3 unités et de petit côté de l'angle droit 1 unité
Une des déterminations de sa mesure (fait Pyth) est la racine carrée de 3²-1²
soit racine carrée de 8.
L'angle au centre qui intercepte l'arc de cercle PP' a pour demi mesure celle de l'angle complémentaire à l'angle PAM, dont le cosinus vaut 1/3
sa mesure est donc π - 2arccosin 1/3
Une des déterminations de la mesure de l'arc du cercle Table intercepté est donc
1 x ( π - 2arccosin 1/3)
Avec les conventions adoptées plus haut,(uddd) la mesure des deux chemins les plus courts est donc (sauf erreur de ma part ... ce qui ne détonnerait pas)
[TeX] 4\sqrt{2} + \pi - 2\arccos\left(\frac{1}{3}\right) [/TeX]
___
Post Scriptum : Ce serait intéressant/rigolo, de redonner le problème avec le rayon ne l'embonpoint de la personne ... un tantinet plus complexe.

 Accueil
Accueil
 Forum
Forum







