 |
#1 - 15-02-2011 11:15:12
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
2 bpules dans un cube
Voici un problème assez sympathique. Pour les adeptes de la logique associée aux mathématiques.
Soient 2 boules de rayon R, dans un cube de coté a.
Trouver a tel que le volume du cube soit le plus petit possible.
#2 - 15-02-2011 11:44:16
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
2 boule sdans un cube
mitsuidewi a écrit:Soient 2 boules de rayon R, dans un cube de rayon a.
Un cube de rayon a ? 
Je pense que tout le monde aura rectifié....
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#3 - 15-02-2011 12:04:55
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
2 boules dabs un cube
oups... dans le feux de l'action la bêtise est maîtresse ! corrigé
#4 - 15-02-2011 13:11:41
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
2 bouleq dans un cube
Ce probleme est l'inverse de Celui la.
La reponse est donc::
r = a * (3−√3)÷4 ou encore a = r* 4 / (3−√3) = r * (2+(2*√3/3))
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#5 - 15-02-2011 13:48:57
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
boules dans un cube
J'ai compris ton énoncé dans le sens: trouver le cube le plus petit possible pouvant contenir 2 boules de rayon R de façon que les boules ne se rentrent pas l'une dans l'autre.
Quand on met une boule de rayon R dans un coin du cube, la distance de son centre au sommet de ce coin est R.racine²(3).
On en déduit que en mettant deux boules dans les 2 coins opposés d'un cube, on peut réduire la grande diagonale du cube à 2.R.(1+racine²(3)).
Le cube a alors un coté valant a=2.R.(1+racine²(3))/racine²(3).
#6 - 15-02-2011 15:19:30
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
2 bouless dans un cube
La boule de centre R, R, R doit passer par le point a/2, a/2, a/2,
point où elle sera tangente à l'autre boule sur la diagonale a, a, a du cube de sommet O.
(x-R)²+(y-R)²+(z-R)²=R² appliqué à ce point donne :
3(a-2R)²=4R²
a-2R=±2R/rac(3) On retient la valeur positive :
a=2R(1+rac(3)/3)=3.155*R environ
#7 - 15-02-2011 16:35:44
- debutant1
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 116
2 boules fans un cube
je trouve le coté du cube C (2c) égal à (r=1)
2c = 2*(1+1/(3^0,5)
je prend un système de coordonnées centré en O centre du cube
par symétrie les sphères sont en contact en O
coordonnées de O1 x= r * cos a * cos b , y = r * cos a * sin b , z = r sin a
par symétrie b= pi/4
sin b= cos b ==1/2^0,5
la sphère touche le coté supérieur du cube
r sin a + r = c
la sphère touche un coté du cube
r cos a cos b + r = a = r cos a * (1/2^0.5) + r
c= 1 + 1/ (3^0,5)
#8 - 15-02-2011 17:29:07
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
2 boules sans un cube
[TeX]R=\frac{3-\sqr3}{4}a\approx=0.317a[/TeX]
The proof of the pudding is in the eating.
#9 - 15-02-2011 19:16:28
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
2 bouels dans un cube
Je propose [latex]a=\frac{2R(sqrt{3}+1)}{sqrt{3}}[/latex]
Je cale mon cube sur les axes avec un sommet en (0,0,0).
Je pars du principe que les deux sphères ont leur centre sur la diagonale intérieure du cube et sont tangentes à trois faces.
La première sphère a donc son centre en (R,R,R) situé à [latex]R sqrt{3}[/latex] de l'origine.
Je rajoute un rayon pour arriver au point de tangence des deux sphères : [latex]R+R sqrt{3}[/latex].
Par symétrie, je double cette longueur et j'obtiens la diagonale du cube: [latex]2(R+R sqrt{3})[/latex]
Je divise la diagonale par [latex]sqrt{3}[/latex] pour obtenir l'arête a.
#10 - 15-02-2011 19:39:04
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
2 boules dans un ccube
Bonjour,
Je dispose les 2 boules dans la grande diagonale du cube.
Cette diagonale vaut aV(1+1+1) soit aV3.
Les cubes se touchent donc cette diagonale vaut aussi RV3+R+RV3.
On aura donc aV3 = R(1+2V3) soit a=R(2+1/V3) ou a=2,577R environ.
Cela ne me semble pas beaucoup: me serais-je trompé ?
Bonne soirée.
Frank
#11 - 16-02-2011 00:24:10
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3620
- Lieu: 94110
2 boules dans un xube
Beau problème, plus difficile que je l'avais imaginé au premier abord ... et qui mérite une petite figure :
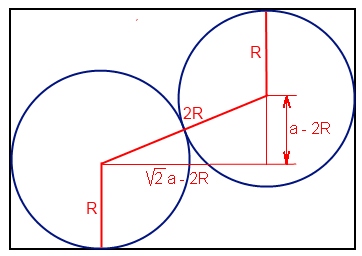
Il reste à résoudre une équation du 2ème degré issue de l'application du théorème de Pythagore et je n'ai jamais été très doué dans le développement de formules un peu compliquées ...
Avec un peu de chance, je dirai :
a = 2.7308 R ?? 
#12 - 16-02-2011 02:41:59
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
2 boules adns un cube
irmo322: Bien joué !
dhrm 77 : je sais bien qu'il s'agit de ton énigme "inverse" mais tu pourrais quand même expliquer comment tu as trouvé ça. autrement c'est la bonne réponse.
halloduda : Méthode originale, mais ca fonctionne !
debutant1 : il faut montrer comment tu as fais.
franck9525 : il y a une erreur, et puis comment fais tu pour obtenir un nombre à la fin alors que j'ai donné des lettres?
loozer : montres comment tu as fais.
franky1103 : revois le cube dans ta tête, tu t'es trompé quelque part.
Jackv : Bonne méthode, mais comme franky1103, tu as dû te tromper dans la disposition des boules.
Je tiens à vous dire que je suis plutôt content de votre participation, c'est ma 1ere énigme et j'avais peur qu'elle fasse un bide totale ^^
#13 - 16-02-2011 09:07:42
#14 - 16-02-2011 09:38:25
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
2 boules dns un cube
mais j'ai bien vu, il me l'a aussi envoyé. Mais plutôt que de montrer un lien, soit vous ne dites rien, soit vous montrez vos résultats.
Ce problème n'est pas tout à fait celui publié par dhrm77, il est même plus simple, alors profitez de la facilité pour donner la réponse, et l'expliquer.
#15 - 16-02-2011 10:14:51
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
2 boiles dans un cube
Le problème de dhrm englobe le tien comme cas particulier.
Si on est plusieurs à te donner le lien c'est que nous on ne voit pas ce que les autres ont écrit...
Et on te le donne pour que tu ne t'étonnes pas que d'autres trouvent facilement.
Ne te vexe pas, en bon matheux on est partisans du moindre effort : si la solution est quelque part et qu'on peut se "ramener au problème précédent", on ne se gêne pas.
Je voulais juste t'informer, c'est tout.
#16 - 16-02-2011 12:37:41
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
2 bouules dans un cube
Ne t'inquiètes pas je n'ai rien contre toi. Je suis sûrement sur la défensive étant donné que c'est ma première énigme. Ça me fait littéralement c**** que mon énigme se trouve dans l'énigme d'un autre. (je ne l'avais pas vu...)
Cependant plusieurs personnes m'ont chacunes donné une méthode différente.
C'est pourquoi tout ceux qui donnent une réponse sans explications, sont encouragés à le faire, pour comparer les méthodes.
#17 - 16-02-2011 12:52:10
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
2 boules ans un cube
Pour l'explication c'est simple, il suffit de determiner les points de contact et de poser les équations. Les détails sont déja donnés sur la deuxieme page de l'autre sujet. Pour 2 boules c'est super-simple, attend de voir pour 18 boules...
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#18 - 16-02-2011 16:38:19
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
2 bouless dans un cube
Bonjour,
Je crois que j'ai vu mon erreur.
J'ai oublié de compter un rayon.
C'est donc a=2R(1+1/V3)=env.3,155R.
Juste cette fois ?
Ca me semble encore faible.
Mais l'intuition est parfois trompeuse.
Bonne journée.
Frank
#19 - 16-02-2011 17:38:17
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3620
- Lieu: 94110
2 bouels dans un cube
OK, j'ai bien vu mon erreur : j'ai considéré que les sphères venaient tangenter les 2 arêtes opposées 
Du coup, les expressions deviennent trop difficiles à manipuler pour ma petite tête : j'abandonne.
Cela reste un excellent exercice, hélas trop fort pour moi.
Merci pour la cogitation.
#20 - 16-02-2011 21:39:06
- yacine97
- Habitué de Prise2Tete
- Enigmes résolues : 10
- Messages : 10
#21 - 16-02-2011 22:46:17
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
2 boules dzns un cube
franky1103 : bravo, cette fois c'est juste, je me disais bien qu'il s'agissait d'un simple oubli.
Jackc : aller un petit effort, tu as bien avance, fais un dessin et mets y toutes les donnees que tu connais.
Yacine97 : il va falloir reflechir plus que ca.
#22 - 18-02-2011 12:27:34
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
2 booules dans un cube
Voici la réponse :
Pour que le cube soit le plus petit possible, il faut que les 2 boules se trouvent sur la grande diagonale. Mais la subtilité est que les boules ne touches pas les arrêtes verticales, voici le dessin :

Pour calculer la distance entre une boule et une arrête, il faut regarder le cube par le haut, on obtient donc :

Le trait bleu représente cette fameuse distance. Je passe les calculs
Pour exprimer a en fonction de R, il suffit de se placer dans le triangle ABC :
D'après Pythagore on a :
[TeX](a-2R)^2+\(a\sqrt{2}-2R\(\sqrt{2}-1\)-2R\)^2 \,=\,4R^2\\
a^2-4aR+4R^2+2a^2-8aR+8R^2=4R^2\\
3a^2-12aR+8R^2=0\\[/TeX][TeX]\Delta = 144R^2-96R^2=48R^2[/TeX][TeX]a_-=\frac{12R-4R\sqrt{3}}{6}=2R(1-\frac{\sqrt{3}}{3})\\
a_+=2R(1+\frac{\sqrt{3}}{3})[/TeX]
Comme [latex]a\> R[/latex] on doit choisir [latex]a_+[/latex].
La réponse est donc [latex]a=2R(1+\frac{\sqrt{3}}{3})[/latex]
Merci à tous ceux qui ont participé à cette énigme.
Vous trouverez également plus d'informations dans cette énigme qui traite le cas de plus d'une boule. http://www.prise2tete.fr/forum/viewtopic.php?id=5143
#23 - 18-02-2011 18:10:28
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
2 boules dans ub cube
Merci pour ta première énigme. Bonne continuation sur le forum 
#24 - 18-02-2011 19:03:44
- gasole
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 1117
- Lieu: Toulouse
2 boukes dans un cube
Quelqu'un connait-il un logiciel libre de géométrie dynamique qui permettrait de modéliser ce problème des deux sphères dans un cube ?
#25 - 18-02-2011 21:04:19
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
2 boules dans un cubz
J'avais essayé plein de logiciel mais c'est la misère... Du coup j'ai utilisé word... Pour le 3D par contre c'est une autre histoire!
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







