Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 20-02-2011 14:39:11
BilardPour continuer la série de vasimolo.... "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#0 Pub#2 - 20-02-2011 16:35:36
bilmardAlors je prends le repère [latex](D,\vec{DC},\vec{DA})[/latex] #3 - 20-02-2011 17:06:27
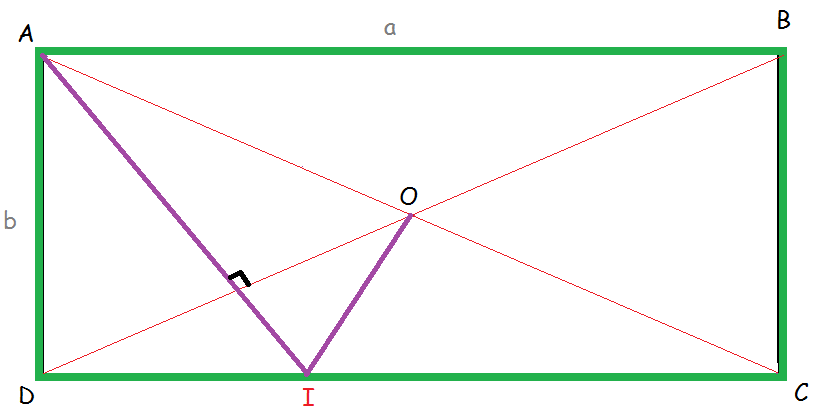
BilalrdEn depliant le billard vers le bas, on trace Le segment OA. The proof of the pudding is in the eating. #4 - 20-02-2011 20:56:24
BilllardAI passe par le symétrique O' de O par rapport à CD. #5 - 20-02-2011 21:48:47#6 - 20-02-2011 23:15:45
biklardAOD est isocèle en O puisque les diagonales du rectangle se coupent en leur milieu et ont même longueur. #7 - 20-02-2011 23:51:28
iBllardPosons c=l'angle ODI #8 - 21-02-2011 11:07:10
BillrdBonjour, #9 - 22-02-2011 01:53:51
billzrdComme le centre de gravité d'une boule de billard rebondit a une distance 'r' du bord d'un billard, on a besoin de la taille de la boule et au moins un coté du billard. Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #10 - 22-02-2011 21:35:33
iBllardSur le plan d'ensemble du billard (qui n'est pas à l'échelle puisque c'est cette échelle que nous cherchons), j'ai tracé trois rectangles bleus. Avoir quatre mains, c'est plus pratique pour taper sur un clavier. #11 - 24-02-2011 17:33:28#12 - 24-02-2011 18:11:21
Billlard
Et quelque soit la manière dont tu joues il y a assez de données dans l'énoncé pour remarquer que la balle par du centre, rebondie et est perpendiculaire à la diagonale et que par conséquent des deux côtés les angles sont les mêmes. "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #13 - 24-02-2011 21:12:55
BilladrTu as raison, toni77 : va jouer. Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.