 |
#1 - 06-02-2010 23:56:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 07-02-2010 12:52:27
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
illard 1
Le billard a un longueur a et une largeur b.
Posons m égal au PGCM de a et de b. Donc m=na=pb.
Pour rendre le problème concret, on suppose que la boule parcourt une diagonale d'un carré unitaire en une seconde.
Toutes les a secondes, la boule change de direction horizontale et toutes les b secondes, elle change de direction verticale. Son parcours finira au moment où elle aurait dû changer de sens horizontalement et verticalement, donc au bout de m secondes.
Si n est pair, elle aura atteint un coin gauche. Si p est pair, elle sera revenue en bas sur le dessin. On peut donc trouver des exemples pour trois des coins, en jouant sur la parité de n et de p... qui doivent être premiers entre eux. La boule ne revient pas au coin de départ car il faudrait n et p pairs.
Exemples pour les autres coins :
* en bas, à droite a=2 & b=1 ... ou a=6 & b=5 (m=30=5a=6b)
* en haut à droite a=1 & b=1 ... ou a=10 & b=6 (m=30=3a=5b)
* en haut à gauche a=3 & b=2 (comme sur le dessin)
Celui qui fuit les casse-tête ne vaut pas un clou.
#3 - 07-02-2010 19:49:17
- Bamby2
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 152
Billar 1
quel que soit la taille, la boule finira toujours par aller dans un coin.
apres pour le prouver oucha 
je dirais simplement sans etre sur de la preuve que si il devait y avoir un chemin ne menant pas a un coin il s'agirait d'un cycle; or ici on part d'un coin, donc on est obligé d'y revenir.
pour pouvoir ne pas fini dans un coin il faudrait ne pas y commencer.
en ce qui concerne le coin d'arrivé, j'y travail, en vain.
#4 - 07-02-2010 23:47:25
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 381
iBllard 1
Oui, ça termine toujours dans un coin :
En effet, la boule touche les bords en un nombre fini de positions (aux intersections du quadrillage), donc si la boule avait une trajectoire infine, elle repasserait 2 fois au même endroit avec la même direction. En repassant le film à l'envers, la boule aurait donc un comportement différent au dernier passage avant de revenir à sa position initiale, ce qui est impossible.
rem : c'est en gros le principe de Fermat du chemin inverse de la lumière.
On suppose que le quadrillage est réduit à 2 entiers premier entre eux.
Si les 2 sont impairs, on s'arrête sur le coin diagonalement opposé.
Si un est pair, on s'arrête sur le coin du coté adjacent de longueur paire.
#5 - 08-02-2010 08:10:51
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
Billarrd 1
Bonjour
Soit l la largeur du tapis de billard et L sa longueur, avec L > l
Soit un repère orthonormé d'origine (0,0) au départ du premier coup
L'axe des abscisses étant orienté dans le sens de la longueur du billard.
Je raisonne avec un tapis virtuellement extensible dans le sens de sa longueur pour s'affranchir des symétries !
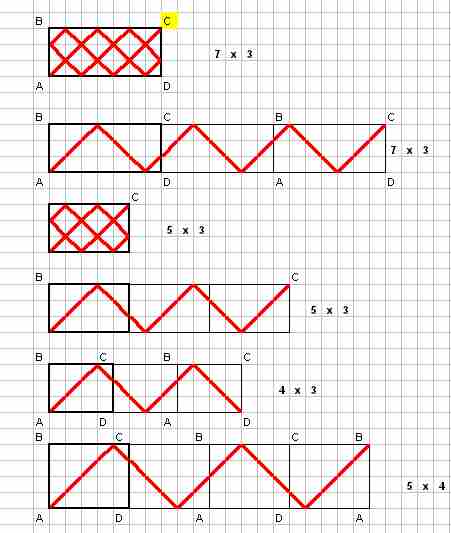
Alors les rebonds (infinis) vont former un "signal triangulaire" de période 2*l et d'amplitude l
Dans ce référentiel, les "trous" se trouvent en (k*L,0) et en (k*L,l) avec k entier naturel.
Ainsi,
Pour que la boule tombe dans un des trous situés aux quatre coins après un envoi à 45°, il faut que :
2* l *i = k*L ou (2*i +1) * l = k*L, (i entier naturel)
c'est à dire que le rapport Longueur /largeur (L/l) soit un rationnel.
Or comme dans l'énoncé, les côtés sont des nombres entiers en cm, cette condition est dont vérifiée et la réponse à la première partie est "oui, tout parcours aura une fin"
Dans quel coin ?
Soit A (0,0), B(0,l), C(L,l) et D(L,0)
(A est le point de départ et B,C,D sont affectés aux trois autres coins dans le sens des aiguilles d'une montre)
Soit a/b la fraction irréductible du rapport L/l
(on note que l'on ne peut avoir a et b pairs simultanément)
Alors si :
a et b sont impairs > la boule sort par le trou "C"
a est pair et b est impair > trou "D"
a est impair et b est pair > trou "B"
(on note en corollaire que la sortie par le trou "A" n'est pas envisageable)
Bonne journée
Nicolas
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#6 - 08-02-2010 11:11:55
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Billard
On consdère "Bord du bas" et "Bord de gauche" comme deux axes d'un repère. On prend comme unité le centimètre.
Supposons (comme ça), que ma balle part d'un point à coordonnées entières avec un angle de 45° avec l'horizontale, le coefficient directeur de la droite suivie est 1 donc la distance parcourue est la même sur les deux axes.
- si elle tape le coté opposé à son point de départ, angles alternes-internes et principe de Descartes appliqué au billard, l'angle de départ après impact sera aussi de 45°
- si elle tape un coté perpendiculaire, la trajectoire est l'hyptohénuse d'un triangle rectangle avec comme angle droit un coin du billard. Un triangle rectangle avec un angle de 45° ? Isocèle rectangle bien sûr, et donc dans ce cas aussi, l'angle de départ sera de 45°
Conclusion 1: l'angle de la balle avec le bord sera toujours, après chaque impact, égal à 45°
- si elle tape le coté opposé à son point de départ, elle aura parcouru une longueur (ou largeur) de billard (soit un nombre entier de centimètres)
- si elle tape un coté perpendiculaire, elle aura parcouru une longueur (ou largeur) de billard moins un certain nombre de centimètres correspondant à sa coordonées de départ (soit un nombre entier moins un nombre entier, donc un nombre entier de centimètres)
Conclusion 2: partant d'un point à coordonnées à valeurs entières, la balle va parcourir un nombre entier de centimètres et arriver en un point lui aussi à coordonnées à valeurs entières.
Prenons maintenant une paire {point d'impact, direction de la balle lorsqu'elle repart}: on prend l'angle dans l'autre sens, on repart du même point, et on trouve facilement le point de départ qui a amené la balle ici.
Conclusion :
- on appelle I l'ensemble des valeurs entières positives ou nulles inférieures à la longueur du bord du bas
- on appelle J l'ensemble des valeurs entières positives ou nulles inférieures à la longueur du bord de gauche
- on appelle A l'ensemble suivant: {45, 135, 225, 315}
- on appelle B l'ensemble des points de départ ou d'impact avec leur angle de trajéctoire, il s'agit de IxJxA moins les valeurs inutiles: toutes les valeurs qui ne sont pas sur un bord, celles qui ont un angle de départ hors du billard, etc...
La fonction f, qui, à un point de départ ou d'impact avec son angle de trajectoire, associe le point suivant avec son angle de départ après impact, est une bijection de B dans B: B est un ensemble fini, à chaque élèment de B, on sait constuire un unique point d'arrivée et un unique point d'origine... (pour le principe, on dira qu'une balle qui va dans un trou repartira comme s'il n'y avait pas de trou)
Une trajectoire complete est définie par la suite U telle que U0 = f((0;0;45)) et Un+1 = f(Un)
Comme f est une bijection d'un ensemble fini vers lui même, il s'agit d'une (ou plusieurs cycles de) permutation. Ce qui est sur, c'est qu'à un moment, on finira par revenir au point de départ...
Ce qui est amusant, c'est qu'on a montré que si la balle ne tombe dans aucun trou avant, elle finira par tomber dans le trou de son point de départ, mais c'est aussi celui dans lequel elle ne tombera jamais 
#7 - 08-02-2010 20:21:36
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 614
villard 1
soit un rectangle n sur m avec p=pgcd(n,m)
Si n=m il va sur la diagonale opposee en 1 coup
On suppose n<m
Si p=1 il va riccocher au maximum n+m fois sur les murs pour arriver sur la largeur opposée d'où est partie la bille
Si p est pair la bille va arriver a l'opposée de la longueur du rectangle d'où la bille est partie
Si p est impair la bille va arriver a l'opposée de la diagonale du rectangle d'où est partie la bille
#8 - 09-02-2010 19:07:51
- MMORgan
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 172
Billad 1
Je n'ai pas envie de mettre en équation toute la trajectoire alors je vais le faire avec des phrases.
Montrons que la bille atteint un coin.
Par l'absurde, supposons qu'il existe une trajectoire où la boule revient de façon périodique. Comme l'angle est à 45°, si on regarde la trajectoire dans le passé, elle va suivre le même chemin (mais dans le sens inverse) et va donc aussi être périodique ! Contradiction avec le fait que cette trajectoire du passé touche le coin bas inférieur.
Où sort-on ?
On ne peut pas sortir par l'endroit où on est rentré, car on doit pour cela repasser par son chemin à un moment et jusqu'à la fin, donc il existe un premier instant où ensuite on reprend le chemin dans le sens passé, et donc à cet endroit l'angle n'est plus de 45°, on est donc déjà dans un autre coin à cet endroit. [c'est pas très clair ça bon toute façon personne ne lira ^^]
On peut sortir par les autres côtés. Je pense qu'il faut regarder, après avoir simplifié la parité (si on a un billard 4*4 c'est pareil que de regarder un 1*1) si on est de la forme :
impair*impair
pair*impair ou
impair*pair.
On peut sûrement utiliser les symétries, mais je n'ai pas de preuve...
En espérant que certains ont calculé toute la trajectoire  (c'est peut-être plus court ^^) (c'est peut-être plus court ^^)
#9 - 10-02-2010 00:24:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
billaed 1
Tout est là ou presque , le PGCD, la parité , la symétrie ...
Pour moi la façon la plus simple de voir les choses est de considérer les symétriques du billard par rapport à la ligne de rebond , la boule continue en ligne doite dans un nouveau billard identique en tout point au premier .

On peut considérer sans problème que les deux dimensions sont premières entre elles ( c'est juste un problème de choix d'unité ) par exemple m de long ( horizontal ) et n de large ( vertical ) . Alors la boule va traverser m lignes horizontales et n lignes verticales avant d'atteindre le sommet opposé du carré . Il suffit de comparer la parité des lignes et colonnes d'arrivées à celles du billard pour conclure .
Merci pour la participation et les idées ...
Vasimolo
#10 - 10-02-2010 10:45:10
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
Billard 11
Je constate avec désarroi que j'ai inventé le PGCM ! Je voulais évidemment parler du PPCM qui correspond justement au nombre de diagonales unitaires parcourues par la boule 
Celui qui fuit les casse-tête ne vaut pas un clou.
#11 - 10-02-2010 12:21:18
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Billaard 1
Propriété 1 :
[TeX]\forall (a,b) \in \left( \mathbb{N}^* \right) ^2, PGCM(a,b) = + \infty[/TeX]

Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#12 - 22-02-2010 02:45:04
Billlard 1
Bonjour,
Vasimolo est ce que tu peux detailler un peu plus ta solution, j'ai rien compris 
Merci
#13 - 22-02-2010 11:36:44
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Billar d1
Je vais détailler sa solution à sa place, j'espère qu'il ne m'en voudra pas...
Au lieu de considérer que la balle rebondit sur une paroi, il peut être plus simple de considérer qu'elle continue sa trajectoire tout droit sur un autre tapis de billard, de taille identique, collé au premier.
Le fait de "déplier" ainsi au fur et à mesure la trajectoire permet de représenter la trajectoire de la boule comme une simple ligne droite, d'angle 45° par rapport aux bords du "tapis", comme montré sur sa figure.
Pour la suite, il suffit de compter le nombre de fois où on a "copié-collé" le tapis dans chaque direction pour savoir dans quel sens roule réellement la boule. Par exemple, "sur l'axe des X", c'est-à-dire de gauche à droite, la boule va vers la droite, bute sur une paroi, va vers la gauche, bute, va à droite, etc. Lorsque l'on "déplie" la trajectoire, elle va toujours vers la droite. Il faut donc compter le nombre de "copier-coller" du tapis de billard qu'on a fait vers la droite : il correspond au nombre de rebonds que la boule a fait dans cette direction. Idem dans l'autre direction, "l'axe des Y", disons.
Enfin, le billard fait m sur n, et vu qu'on part à un angle de 45°, on parcourt un centimètre "vers la droite" en même temps qu'un centimètre vers le haut. On arrive donc à un angle lorsque l'on a parcouru un certain nombre de fois m centimètres, et en même temps un certain nombre de fois n centimètres ; on a donc parcouru un nombre de centimètres qui est à la fois multiple de m et de n, et le plus petit nombre qui respecte ces conditions est, non pas [latex]m \times n[/latex], mais PPCM(m,n) (le plus petit commun multiple, comme son nom l'indique...  ) Plus qu'à voir par combien on multiplie m (ou n) pour parvenir à PPCM(m,n), et on sait combien de fois la boule a rebondi sur une paroi verticale (ou horizontale), et donc dans quel sens elle allait juste avant de buter contre un coin : on connaît donc ce coin ) Plus qu'à voir par combien on multiplie m (ou n) pour parvenir à PPCM(m,n), et on sait combien de fois la boule a rebondi sur une paroi verticale (ou horizontale), et donc dans quel sens elle allait juste avant de buter contre un coin : on connaît donc ce coin 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#14 - 22-02-2010 18:43:58
illard 1
Merci pour ton explication, c'est plus clair en effet même si je vois pas encore trop comment j'aurai pu y penser... peut être en faisant un dessin...
#15 - 22-02-2010 21:12:54
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
Billardd 1
l'entrainement, l'entrainement...
http://enigmusique.blogspot.com/
#16 - 22-02-2010 21:59:01
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Billaard 1
Ovni a écrit:Merci pour ton explication, c'est plus clair en effet même si je vois pas encore trop comment j'aurai pu y penser... peut être en faisant un dessin...
NickoGecko a écrit:Je raisonne avec un tapis virtuellement extensible dans le sens de sa longueur pour s'affranchir des symétries !
Ceci dit, je n'avais pas trouvé, et n'avais pas non plus pensé à "étendre" le tapis... mais je comprends qu'on ait pu y penser pour résoudre 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#17 - 22-02-2010 22:01:04
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
billaed 1
Pour le problème de l'araignée dans un cube (c'est Gaby qui l'a posé ici il me semble), on fait pareil.
http://enigmusique.blogspot.com/
#18 - 22-02-2010 22:02:17
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Billarrd 1
Bonne mémoire... Encore une énigme à laquelle tu n'as rien répondu, mais à laquelle, a posteriori, tu as compris quelque chose. Encore un point commun entre nous 
Pour l'araignée dans la pièce :
L'originale
La variante
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#19 - 19-02-2011 01:46:24
- scheumele
- Amateur de Prise2Tete
- Enigmes résolues : 9
- Messages : 2
bimlard 1
Si les angles sont parfaitement a 45° ET que la boule garde toute son énergie, alors il s'agit d'un mvt perpétuel donc NON . Si il y a perte d'énergie, alors la boule s'arretera toute seul et pas forcement ds un coin.
#20 - 19-02-2011 11:43:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
billars 1
Relis la question 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









