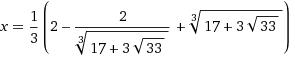Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 10-06-2011 21:19:14
avec les fonctoons ...Soit [latex]f[/latex] une application de [latex]R[/latex] vers [latex]R[/latex] telle que : "Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#0 Pub#2 - 10-06-2011 21:56:53
Avec Les fonction s...f(x) = a x avec a^4 = a^3 +2 soit , a=-1 : f(x) = -x #3 - 10-06-2011 22:11:46
Avec Les foncttions ...Soit a une solution de l'équation a^4=a^3+2 (cette équation a deux solutions, l'une positive, l'autre négative). #4 - 10-06-2011 23:55:29
Avec Les fontcions ...J'ai pensé à une fonction tout simplement linéaire, de la forme [latex]f(x) = kx[/latex] (qui est bien une application de [latex]\mathbb{R}[/latex] vers [latex]\mathbb{R}[/latex], avec k un réel. En remplaçant l'expression de la fonction dans [latex]fofofof(x)=fofof(x)+2x[/latex], on a : #5 - 13-06-2011 09:48:43
Avec Les fonctiions ...On va faire simple : f(x) = -x est une solution #6 - 13-06-2011 12:00:28
avec les donctions ...je proposerais bien :[latex]f(x)=-x[/latex] Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.