 |
#1 - 09-07-2011 18:15:15
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
DD'entiers
Les longueurs des segments tracés sont toutes entières et différentes (sauf contre-indication explicite).
Que vaut le périmètre minimum du polygone gris?
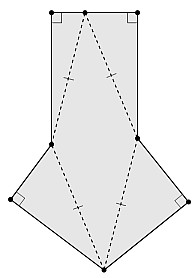
Quelques remarques suite aux erreurs et questions :
Spoiler : [Afficher le message]
1. Les deux segments du dessus sont alignés mais chacun a une longueur entière.
2. Le losange central a, lui aussi, des côtés de longueur entière.
#2 - 09-07-2011 18:26:05
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
d'entizrs
Cherche-t'on quatre triplets de Pythagore qui aient leur plus grand élément en commun ?! Pfiouh o_O'
Du coup, au détour d'une page Web (celle-ci) qui liste des triplets pythagoriciens, je fouille, et je trouve ces quatre triplets :
(39 ; 52 ; 65)
(33 ; 56 ; 65)
(25 ; 60 ; 65)
(16 ; 63 ; 65)
Il ne me semble pas qu'on puisse trouver moins que 65, donc le périmètre minimum du losange de la figure semble être 260.
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#3 - 09-07-2011 18:35:54
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
D'entieers
C'est ça Mathias, mais pas obligé de le faire à la main 
#4 - 09-07-2011 20:17:40
- clement.boulonne
- Passionné de Prise2Tete
- Enigmes résolues : 28
- Messages : 64
D'entieers
Les hypoténuses des triangles rectangles sont tous égales ou ?
#5 - 09-07-2011 20:22:16
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,195E+3
d'entizrs
Pour avoir les deux triangles rectangle du bas , 3-4-5 ou 8-6-10 , 5-12-13 ... toujours une seule solution....
Le premier entier admettant deux solutions entières est 25 pour le losange.
Pour les dimensions en bas : 7 et 24 , 15 et 20 .
Ce qui donne en haut : "je cherche encore  " (Je dirais 19 20 21 à vue de nez en divisant 2*625 par 3) " (Je dirais 19 20 21 à vue de nez en divisant 2*625 par 3)
#6 - 09-07-2011 21:09:24
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
D'eniers
@clement.boulonne : oui
@gwen27 : tu es sur la bonne voie, mais à la main ça va être pénible.
#7 - 09-07-2011 21:20:01
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,195E+3
d'ebtiers
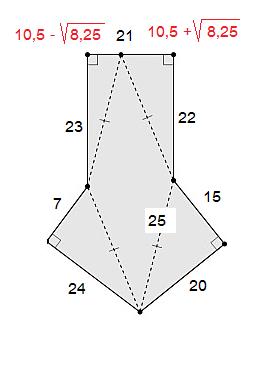
Périmètre : 20+15+24+7+21+22+23 = 132
#8 - 10-07-2011 08:42:10
- Memento
- Professionnel de Prise2Tete
- Enigmes résolues : 30
- Messages : 176
D'enteirs
Je propose 444. Comme l'on sait qu'il y a 4 triangles rectangles, avec des longueurs entières, il suffit de chercher les premiers triplet pythagoriciens ayant la même longueur c (hypothénuse). J’espère juste ne pas en avoir oublié 
#9 - 10-07-2011 12:16:35
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
d'entierd
Il s'agit de trouver un entier qui apparaît dans au moins 4 triplets pythagoriciens (A046081).
Le plus petit entier répondant à ce critère est 12, avec les triplets (5,12,13), (9,12,15), (12,16,20) et (12,35,37).
C'est lui qui donne a priori le plus petit périmètre avec 150.
Après un MP de looozer, je me sens un peu crétin de mon erreur.
Bon je recommence :
Il s'agit de trouver un entier qui apparaît comme longueur de l'hypothènuse dans au moins 4 triplets pythagoriciens (A046080).
Le plus petit entier répondant à ce critère est 65, avec les triplets (39,52,65), (33,56,65), (25,60,65) et (16,63,65).
C'est lui qui donne a priori le plus petit périmètre avec 344.
Très sympa.
(et j'adore le titre, même si ça n'a pas grand chose à voir avec l'énigme ^^)
#10 - 10-07-2011 12:29:55
- bidipe
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1126
- Lieu: Côte basco-landaise
d'ebtiers
Si j'ai bien compris, il faut que je donne la valeur 4X
où X satisfait les égalités : X² = A²+B² = C²+D² =E²+F² = G²+H²
avec A, B, C, D, E, F et G entiers distincts
Faut que je retrouve les quelques notions de python que j'avais apprises en autodidacte pour des énigmes il y a 2 ans, et ca c'est pas gagné  
A moins qu'en fouillant dcode, notre ch'Ef' bien aimé ait pondu un truc pour trouver çà...
#11 - 10-07-2011 14:32:41
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
D''entiers
Bravo à MthS-MlndN, seul à avoir trouvé pour l'instant.
#12 - 10-07-2011 15:34:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,195E+3
d'enyiers
Le trait en haut était trompeur... Alignés, on pouvait ruser 
Mais bon, le minimum devient un losange de 63 de côté
Ce qui donne des triangles rectangle d'hypothénuse 63 (le premier à 4 décompositions différentes) de côtés : (16-63) (25-60) (33-56) et (39-52)
Soit un périmètre de 344 Je préférais "tricher" avec 132 
#13 - 10-07-2011 16:21:07
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
D'eentiers
C'est vrai, personne d'autre n'a trouvé ? o_O'
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#14 - 10-07-2011 18:56:31
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
D'entier
Encore deux bonnes réponses de FRiZMOUT et gwen27.
#15 - 10-07-2011 19:23:38
- Yanyan
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 509
- Lieu: Lille si j'y suis
D'netiers
La réponse est en lien avec l'entier n² le plus petit se décomposant en somme de huit carrés distincts.
Je n'ai pas encore trouvé cet entier.
Un mathématicien complet est topologiquement fermé!
#16 - 11-07-2011 20:53:24
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
d'entierd
Le losange a pour côté 1105 au minimum, 1105 étant le premier quadruplet de triangle pythagorien, le suivant est 1625.
Le périmètre du losange est donc 4420, son aire 341887.
Edit:
J'ai en fait généré une liste de triplets incomplète en utilisant la méthode suivante:
Soient u et v entiers, u>v on obtient x=u²-v², y=2uv et z=u²+v²
Cette méthode permet de générer (3,4,5), (6,8,10) ou (12,16,20) mais pas (25,60,65) ??
En utilisant une liste complète de triplets générée par internet, j'obtiens les quatre triangles
16 63 65
25 60 65
33 56 65
39 52 65
ce qui fait un périmètre de 260.
The proof of the pudding is in the eating.
#17 - 13-07-2011 12:29:47
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
D'eentiers
Il doit y avoir une ruse que je ne vois pas??
Je nomme les longueur des segments a,b,c,d,e,f,g,h en partant du point en haut au centre et en tournant dans le sens trigo et l la longueur du côté du losange.
Je cherche 4 triplets de pythagore dont le 3ème terme est le même:
[TeX]a^2+b^2=l^2[/TeX]
[TeX]c^2+d^2=l^2[/TeX]
[TeX]e^2+f^2=l^2[/TeX]
[TeX]g^2+h^2=l^2[/TeX]
Avec les conditions: a,b,c,d,e,f,g,h,l et a+h tous différents (faut-il inclure a+h)?
Je trouve:
(16,63,65)
(25,60,65)
(33,56,65)
(39,52,65)
a+h dépend du placement des côtés.
Pour ressembler le plus à la figure présentée ci-dessous (tailles dans le même ordre), on peut donc prendre par exemple les côtés dans l'ordre suivant:
16,63,33,56,52,39,60,25
Dans ce cas le segment du haut entre les points extrèmes vaut 41 qui est bien différent des autres.
On demande le périmètre: 16+63+33+56+52+39+60+25=344
Amusant comme énigme. Merci.
La forme me fait penser à un calamar. C'est grave docteur?
#18 - 13-07-2011 14:02:55
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
d'entoers
Sauf erreur de calcul, j'en suis à 29286.
Les triangles sont homothétiques des suivants :
25²=15²+20² soit 5525²=3315²+4420²
25²=7²+24² soit 5525²=1547²+5304²
13²=5²+12² soit 5525²=2125²+5100²
17²=8²+15² soit 5525²=2600²+4875²
Les hypoténuses font 25x13x17=5525 (ppcm)
Les longueurs des côtés sont bien entières et distinctes
Le périmètre fait 13x17(15+20+7+24)+13x25(8+15)+17x25(5+12)
=14586+7475+7225=29286
=3315+4420+1547+5304+2125+5100+2600+4875
#19 - 13-07-2011 14:48:42
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
D'enters
Bonnes réponses de franck9525 et rivas
(certains donnent le périmètre du losange, d'autres celui du polygone "calamar", mais ce n'est pas là l'important)
halloduda : tes réponses sont trop grandes.
#20 - 13-07-2011 15:04:04
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
D'eniers
Bonjour,
On cherche quatre triplets pythagoriciens [(x;y;z) tel que x²+y²=z²] de même z, avec x et y tous différents.
Avec Excel, j'établie un tel tableau [x=2np ; y=n²-p² ; z=n²+p²], je trie les données par rapport à z et je regarde quand on a pour la première fois 4 fois le même z: je trouve z=65.
Le périmètre minimum vaut donc 260, mais je ne suis pas sur d'être dans le vrai.
Par ailleurs, ma méthode me semble trop empirique pour être "acceptable".
Bonne journée.
Frank
Edit: texte modifié (il y avait une plus petite valeur répondant à la question)
#21 - 13-07-2011 17:57:21
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
D'entieers
Je dirais 5568.
1105²=1073²+264²=817²+744²=1104²+47²=576²+943².
Le 1105 se calcule comme le produit des 3 triangles rectangles minimaux différents:
(3,4,5) (5,12,13) (8,15,17).
#22 - 13-07-2011 18:13:49
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
d'entirrs
Franky1103 et nodgim, vous pouvez faire plus petit.
#23 - 13-07-2011 23:42:48
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
'entiers
C'est ok pour Franky1103 aussi.
#24 - 14-07-2011 21:19:40
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
D'enters
Merci à tous d'avoir participé à mon énigme 
Bravo à ceux qui ont trouvé 344 comme périmètre du polygone gris (j'ai accepté aussi 260 pour le périmètre du losange).
Une difficulté venait de la présence de listes ou de méthodes incomplètes sur le Web. De même, il existe des triplets primitifs (nombres premiers entre eux) et d'autres qui en sont des multiples. C'était le cas avec (25, 60, 65) qui découle de (5, 12, 13).
#25 - 15-07-2011 07:15:00
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
D'entiiers
Pour en finir avec l'usage de l'informatique sur ce sujet et pour expliquer ce qui se passe:
Tout d'abord, tout nombre premier de forme 4k+1 est somme de 2 carrés de manière unique (c'est du Fermat je crois):
5=1²+2²
13=2²+3²
17=1²+4²
etc...
D'autre part, le produit de 2 nombres somme de 2 carrés est lui même somme de 2 carrés:
Si p1=a²+b² et p2=c²+d²
p1*p2=(ac+-bd)²+(ad+-bc)² ce qui donne 2 solutions si p1 et p2 différents.
Mais si p1=p2 alors un seul résultat est valable:
p=a²+b² et donc p²=(a²-b²)²+(2ab)²
Donc pour trouver la décomposition en somme de 2 carrés d'un carré d'un nombre premier p², p de forme 4k+1, il suffit de trouver la décompo de p. Pour cela aligner les n² succéssifs modulo p et trouver les 2 premiers nombres opposés.
Pour 29 par exemple:
1 4 9 16 25.. se traduit modulo 29 en :1 4 9 -13 -4
4 et -4 étant opposés, leur somme est nulle modulo 29, leur somme vaut 29:
29=5²+2²
et donc 29²=(5²-2²)+(2*2*5)²=21²+20²
On arrive donc rapidement à trouver la décompo de 5², 13², 17², 29², etc...
et donc les triplets des triangles entiers dont on a besoin:
(3,4,5)(5,12,13)(8,15,17)....
Ensuite pour trouver les combis, il suffit soit de multiplier terme à terme:
pour 5*13=65 on multiplie (3,4) par 5 et (5,12) par 13 et donc ça donne les 2 triplets nouveaux (39,52,65) et (25,60,65).
Soit d'utiliser la forme décrite ci dessus (ac+-bd)²+(ad+-bc)² ce qui donne 2 autres triplets (16, 63, 65) et (56,33,65).
Donc pour un nombre P qui est produit de n nombres premiers de forme 4k+1, alors le nombre de triangles rectangles dont P est l'hypothénuse vaut:
(3^n-1)/2.
13 pour un produit de 3 nombres, 41 pour 4 nombres, 121 pour 5 nombres.....
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








