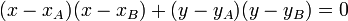Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 04-09-2011 21:36:33#0 Pub#2 - 04-09-2011 21:46:16
au careé ![TeX]2r[/latex], avec [latex]r[/latex] le rayon du cercle. Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #3 - 04-09-2011 22:06:10
Au caré !Bonjour, #4 - 04-09-2011 22:46:00#5 - 05-09-2011 03:02:33#6 - 05-09-2011 09:45:00#7 - 05-09-2011 09:58:48#8 - 05-09-2011 10:23:28#9 - 05-09-2011 11:23:35
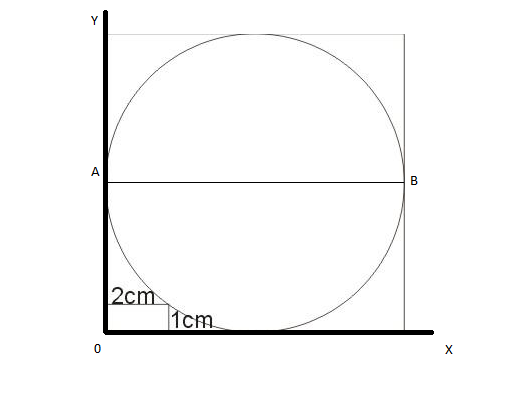
Au carr !On pose O le centre du cercle, on trace un repère dont les axes sont parallèles aux cotés du carré, et on note R le rayon du cercle (ou le demi côté du carré). #10 - 05-09-2011 12:04:35
Au carr é!Plaçons un repère au centre du cercle (et du carré), l'unité étant le centimètre. #11 - 05-09-2011 12:52:16
ay carré !Si je note r le rayon du cercle, on peut utiliser Pythagore dans un triangle dont 2 des côtés sont le centre du cercle et le sommet du rectangle qui est situé à l'intérieur du carré. #12 - 05-09-2011 16:11:50
AAu carré !Ça vaut 10 très cher SaintPierre. #13 - 05-09-2011 19:53:25#14 - 05-09-2011 21:30:04
Au caré !Aucun problème. Bravo à tous ! C'est à l'intelligence d'achever l'oeuvre de l'intuition. Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.