Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 25-09-2011 16:43:17
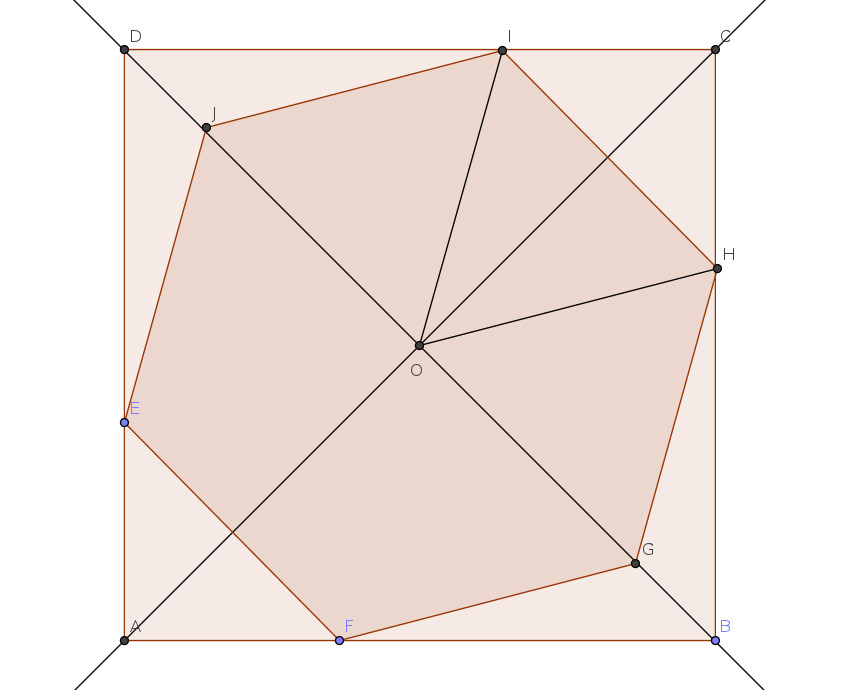
'Hexa-goneL'autre jour, notre prof de maths nous a donné un carré de papier de 10 cm de longueur exactement. Un promath- actif dans un forum actif
#0 Pub#2 - 25-09-2011 17:34:52
L'Hexa-gnoe[TeX]r=\frac{10\sqrt2}{\sqrt3+1}\approx5,18cm[/TeX] #3 - 25-09-2011 18:52:03#4 - 25-09-2011 18:52:56
L'HexagoneUne belle question. The proof of the pudding is in the eating. #5 - 25-09-2011 19:21:50#6 - 25-09-2011 19:38:30#7 - 25-09-2011 19:52:54#8 - 25-09-2011 20:46:54#9 - 25-09-2011 21:58:48
L'Hexa-gneOn peut dire que ce problème m'a donné du mal. #10 - 25-09-2011 22:45:08#11 - 26-09-2011 06:44:19#12 - 26-09-2011 17:11:45
L'Hexa-gon5,17cm. Il faut tourner l'hexagone de Pi/12 par rapport à ce qu'on fait les autres élèves, cela revient à faire passer une des diagonales du carré par deux sommets de l'hexagone. #13 - 26-09-2011 17:28:08#14 - 28-09-2011 17:00:49
L'Heexa-goneFinish! Un promath- actif dans un forum actif Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | ||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.