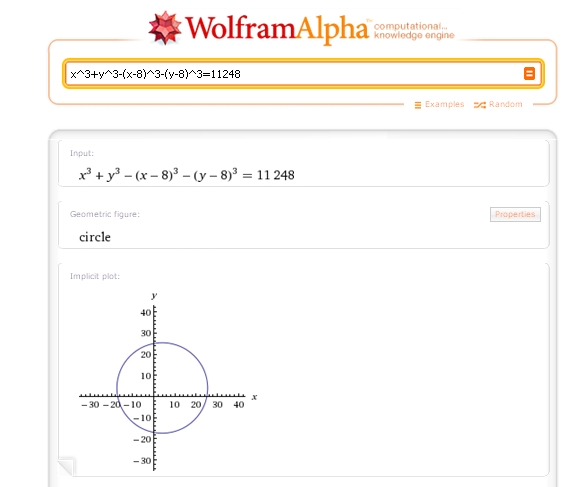
|
#1 - 26-09-2011 20:19:01
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Les pierres brisées (Recitfié)
Le gouvernement vient de trouver une nouvelle sorte de pierre: L'oster. Cette pierre a la particularité d'être très explosive et les plus grandes pierre oster font maximum 100g.
Pour trouver la valeur d'une oster, on met sa masse au cube (ex: 3g=3*3*3=27euros) puis on met en euros.
Un employé manipulait 2 pierres d'oster dans ses mains, qui avaient un poids en grammes exact ( il n'y avait pas de décimales à son poids.)
Mais les pierres ont explosé dans ses mains.
Chacune des pierres a perdu 8 grammes, ce qui represente une perte de 11248 euros au total.
Frustré, son patron l'a viré pour une telle somme. Il lui a dit:
"Tu nous a fait perdre 11248euros!"
Ensuite, l'employé s'est demandé quelles étaient les masses des deux pierres avant l'explosion.
Alors, Quelles étaient les masses des deux pierres avant explosion?
Bon courage... je suis fier de la difficulté.
on répondra sous forme:
1g;2g
Un promath- actif dans un forum actif
#2 - 26-09-2011 20:39:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Les ppierres brisées (Rectifié)
Peux tu expliciter "chacune des pierres a perdu 8 grammes" ?
Dans l'explosion ? Il reste donc quelque chose des pierres qui ont explosé ?
Merci d'avance
#3 - 26-09-2011 21:30:20
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Les piierres brisées (Rectifié)
Wolfram alpha me dit : pas de solution entière.
#4 - 26-09-2011 21:35:57
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Les pierres brisées (Rctifié)
Euh... Si une pierre qui pesait [latex]x[/latex] ne pèse plus que [latex]x-8[/latex], la perte est de [latex]x^3-(x-8)^3[/latex] euros, et ce nombre est toujours pair, donc je ne vois pas comment trouver une solution à ton problème.
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#5 - 26-09-2011 21:55:56
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
Les pierres brisées (Rectfié)
Bonjour
Un oster de x grammes vaut x^3 euros.
S'il perd 8 grammes, il vaut (x-8)^3 euros.
La perte est donc 24x^2 - 192x + 512 euros.
Même chose pour celui de y grammes qui perd 24y^2- 192y + 512 euros.
L'équation à résoudre est :
24 x^2 + 24y^2 - 192x - 192y + 1024 = 11248
Après réduction et division par 24, il vient :
X^2 - 8x + y^2 - 8y = 426
qu'on transforme en
(x - 4)^2 + (y - 4)^2 = 458
Or 458 = 17^2 + 13^2
On peut donc dire qu'une pierre pèse 21 grammes et l'autre 17 grammes
#6 - 26-09-2011 22:07:37
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
Les pierres brisées (Rcetifié)
Bjr Promath (et les autres),
Après >35min sous Excel, en tentant de résoudre :
(Ai^3)-(Ai-8)^3 +(Bi^3)-(Bi-8)^3-11717=0
...puis avec Wolfram
http://www.wolframalpha.com/input/?i=%2 … ^3%3D11717
En vain...
Je n'ai hélas pas pu trouver de valeurs entières...?!
À suivre

#7 - 26-09-2011 22:13:14
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Les pierres brisées (Rectifiié)
Il me semble que la somme perdue devrait être paire, non ?
_____________________
Après correction de l'énoncé, je trouve finalement la seule solution :
17g et 21g
Le prix initial était de 14174€, et n'est plus que de 2926€, soit bien 11248€ de moins.
#8 - 26-09-2011 22:31:20
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
les pierres brisées (eectifié)
La différence entre le cube d'un nombre et le cube de (ce même nombre -8) ne peut être que paire... 11717 étant impair, pas de solution possible.
Là, c'est plus raisonnable : Les poids sont forcement compris entre 8 et 25 grammes.
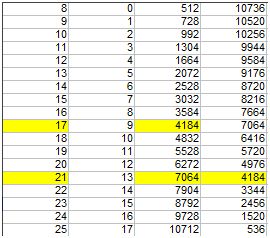
En cherchant les compléments, on trouve un couple unique : 21 et 17 g
#9 - 27-09-2011 06:46:40
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Les pierres brisées (RRectifié)
En refaisant mon problème, je trouve la solution:
Précision:
1°LES 2 PIERRES ONT EXPLOSE
2°11248 EST BIEN LE TOTAL PERDU;
en esperant avoir été clair...
Un promath- actif dans un forum actif
#10 - 27-09-2011 06:49:17
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
eLs pierres brisées (Rectifié)
Pardon, je ne sais plus compter... Au lieu de soustraire 8 , j'ai soustrais 7.
Je modifie...
Je suis complètement ebahi...
W******* peut faire les equations!
Un promath- actif dans un forum actif
#11 - 27-09-2011 11:15:10
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Les pierres briséess (Rectifié)
17 Grammes et 21 Grammes .
17^3 + 21^3 - 9^3 - 13^3 = 11248
Merci pour cette enigme
Azdod
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#12 - 27-09-2011 14:24:21
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
Les pierres brisées (Retifié)
#13 - 27-09-2011 15:52:42
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Less pierres brisées (Rectifié)
Soit x et y les masses des pierres avant l'explosion.
On cherche x et y tels que:
[TeX]x^3-(x-8)^3+y^3-(y-8)^3=11248[/TeX]
Soit: [latex]8(3x^2-24x+3y^2-24y)=10224[/latex]
Soit: [latex]x^2-8x+y^2-8y=426[/latex]
Soit: [latex](x-4)^2+(y-4)^2=458[/latex]
Soit en posant X=x-4 et Y=y-4:
[TeX]X^2+Y^2=458[/TeX]
X et Y étant entiers, et chacun plus petit (strictement) que 22, la recherche n'est pas longue: On trouve 13 et 17 pour X et Y, soit 17 et 21 pour x et y.
Les solutions sont donc 17g et 21g validées par la case réponse.
Merci pour cette énigme.
#14 - 27-09-2011 17:07:06
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Lse pierres brisées (Rectifié)
Bravo... La réponse est celle ci...
C'est vrai qu'avec W******* **** ca change tout...
Un promath- actif dans un forum actif
#15 - 27-09-2011 19:15:59
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Les pierres briséees (Rectifié)
Euh, je n'ai pas eu besoin de Wolfram pour simplifier l'expression ni pour résoudre [latex]X^2+Y^2=458[/latex] en entier. Il suffit de jeter un oeil rapide à une table de carrés de 1 à 21. 
#16 - 27-09-2011 19:45:26
- papiauche
- Sa Sainteté
- Enigmes résolues : 49
- Messages : 2131
Les pierres bbrisées (Rectifié)
C'est sûr que W***, ça dégage 
En deux coups de cuillère à pot, on trouve:
17 et 21 g.
"Je ne lis jamais un livre dont je dois faire la critique. On se laisse tellement influencer." O. Wilde
#17 - 27-09-2011 19:55:04
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
les pierres brisérs (rectifié)
Pas facile...
Juste une question: les nouvelles pierres (qui résultent de l'explosion) ont aussi un poids en gramme exact?
#18 - 28-09-2011 05:46:11
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
Les pierres risées (Rectifié)
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#19 - 28-09-2011 06:54:58
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Les pieres brisées (Rectifié)
Barvo
@ irmo Si elles perdent exactement 8 grammes, alors...
Un promath- actif dans un forum actif
#20 - 28-09-2011 07:38:32
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
Les pierres briséées (Rectifié)
Ok, c'est juste que je pensais qu'une pierre pouvait exploser en plusieurs morceaux.
Par exemple la première pierre fait vingt grammes, elle explose en deux pierres de 5,5g et 6,5g, elle a donc globalement perdu 8 grammes.
Vu comme ça le problème se complique pas mal!
#21 - 28-09-2011 09:45:06
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Les pierres briséess (Rectifié)
Soient x et y les deux masses.
EDIT après correction faute de calcul
On a perdu x³+y³-(x-8)³-(y-8)³=11248 €.
soit 24x²-192x+24y²-192y+2x512=11248
ou x²+y²-8(x+y)=426
qui peut s'écrire
(x-4)²+(y-4)²=426+2x16=458
solution x-4=17 ; y-4=13
On trouve x=21g, y=17g.
#22 - 28-09-2011 11:17:05
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Les pierres brisées (Retifié)
On note les deux poids a et b. On a:
a^3 + b^3 - (a-8)^3 - (b-8)^3 = 11248
24a² - 192a + 512 + 24b² - 192b +512 = 11248
a²+b² - 8(a+b) = 426
A partir de là, on peut tatonner, mais je préfère une autre méthode:
On pose S = a+b; P = a.b
a²+b² - 8(a+b) = 426
a²+b²+2ab -2ab - 8(a+b) = 426
(a+b)² - 8(a+b) -2ab = 426
P=S²/2-4S-213
On peut donc trouver a et b en fonction de S via l'équation du second degré suivante:
X²-SX+S²/2-4S-213 = 0
Delta = S²-2S²+16S+852 = 16S+852-S²
Ce Delta est un carré parfait en théorie, donc on aurait
S²-16S-852+q² = 0
DeltaBis = 256 + 3408 - 4q² = 4(916-q²)
S vaut donc 8 +/- sqrt(916-²q). Comme les 2 pierres ont perdu 8 grammes chacune, alor s > 8 donc
S = 8 + sqrt(916-q²)
Du coup, a et b valent:
a = (8 + sqrt(916-q²) - q)/2 et b = (8 + sqrt(916-q²) + q)/2
Reste plus qu'à identifier q. On sait que z²+q² = 916 = 2.2.229
Le théormème des 2 carrés nous indique qu'il n'y a que deux solutions: q=4 ou q=30 (et z=30 ou z=4)
On élimine le cas q=30 (a serait négatif); donc q=4.
On trouve donc: a=(8+30-4)/2 = 17 et b= (8+30+4)/2 = 21
La réponse est donc 17 et 21 grammes
#23 - 28-09-2011 12:17:13
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Les perres brisées (Rectifié)
Est-ce que apres l'explosion les 2 pierres deviennent 4 pierres (dont 2 de 8 grammes)? ou les 16 grammes s'évapore?
edit...
apparement les 8 grammes s'evaporent, sinon il n'y a pas de solution.
La solution est 17 et 21.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#24 - 28-09-2011 12:24:02
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
les pierreq brisées (rectifié)
irmo: elles explosent en 1 pierre chacune
halloluda: Non
scarta: Bravo!
dhrm77: après l'explosion chacune des pierres a perdu 8 grammes, mais les 8 grammes s'évaporent, il y a donc -16 grammes au total.
Un promath- actif dans un forum actif
#25 - 28-09-2011 12:41:21
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Les pierres brisées (Reectifié)
Avec un tableau a double entrée sur tableur, on trouve facilement 17 et 21 grammes.
Sinon ça revient à résoudre dans N l'équation : x²+y²-8(x+y)=426
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum