 |
#1 - 30-06-2012 10:19:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#2 - 30-06-2012 10:44:54
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,985E+3
Déés 2
Tu n'y arriveras pas :
Le "remplissage" des 8 sommets implique d'utiliser 8 centres d'arête différents.
Le "remplissage" des 6 centres des faces en nécessite 6 de plus.
Or, on n'a que 12 centres d'arête et non 14.
#3 - 30-06-2012 10:45:35
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
sés 2
Salut,
Ba tu va pas! :p
Coloriage en damier noir et blanc de la forme à construire et on trouve 14 cubes noir et 12 cubes blanc (ou le contraire). Une bûchette se plaçant nécessairement sur 2 cubes de couleurs différentes c'est impossible.
#4 - 30-06-2012 12:41:25
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
déd 2
Tu utilises quel logiciel pour faire d'aussi beaux dessins? Que je puisse répondre à la question de manière compréhensible 
Shadock
PS : Je verrai plus tes ce "Dés 2" dans énigme logique.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#5 - 30-06-2012 13:47:31
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Déés 2
On peut prouver que ce n'est pas possible. Si je colorie de 2 couleurs differentes (rouge et bleu par exemple) les petits dé qui constituent le grand cube de telle maniere que les buchettes qui le composerais soient toujours conposées d'un bleu et d'un rouge... alors on colorie a la maniere d'un echequier en 3 dimensions. Si les coins sont bleus, le centre du cube est rouge. si on retire le centre, on aurait 14 bleus et 12 rouges. Or chaque buchette doit avoir un bleu et un rouge. Pour que se soit possible Il nous faudrait 13 rouges et 13 bleus.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#6 - 30-06-2012 14:21:36
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
éDs 2
Intuitivement, cela semble impossible (sinon, la solution serait triviale) mais je ne pense pas pouvoir le prouver.
#7 - 30-06-2012 14:52:16
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Dés
Bon courage.
Ça m'étonnerait que tu y arrives !
Si tu colories les cubes comme aux échecs, tu dois employer 14 cubes blancs et 12 noirs.
Tes buchettes ne peuvent être constituées que d'un cube blanc et d'un noir.
Avec tes buchettes, tu ne peux faire que le même nombre de noirs et de blancs.
#8 - 30-06-2012 19:10:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dés
Un premier point .
Clydevil , Dan , Halloduda : c'est bon !
Gwen : oui . Question bonus : et si le cube fait 5X5X5 ?
Les autres : c'est ça il reste à le montrer .
Vasimolo
#9 - 30-06-2012 20:29:05
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,985E+3
Dé s2
Gwen : oui . Question bonus : et si le cube fait 5X5X5 ?
Ca ne change pas grand chose, mais il faut raisonner un peu autrement.
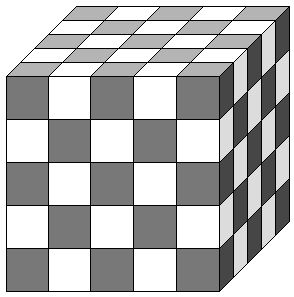
Je fais ça par couches successives en coloriant mon cube comme un échiquier.
La face de dessus, j'ai 13 cases blanches pour 12 noires
La tranche en dessous, il y a donc une case noire de prise (ou 2 noires et une blanche....) Enfin bon ça fait une noire de moins.
idem pour les deux étages suivants du coup.
Si bien qu'à la dernière face j'ai 11 noires pour 13 blanches. Ca ne peut pas coller. (ou 10 pour 12 , 9 pour 11 .... suivant les options de remplissage vertical.
En fait, il y a même plus simple :
Sur un cube de dimension impaire, il y a toujours 2 cases noires en plus des blanche, du fait des damiers supérieurs et inférieurs.
#10 - 30-06-2012 22:48:57
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
Déss 2
Il faut 8 doubles dés pour les 8 angles. Mais aussi 6 autres pour le milieu des faces.
8+6=14.
ça ne colle pas avec 13 doubles dés.
#11 - 30-06-2012 23:21:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Déés 2
Oui Nodgim et je te propose le même bonus qu'à Gwen ( qui a bien répondu ) : avec un dé 5X5X5 ?
Vasimolo
#12 - 01-07-2012 00:45:06
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Dés 22
Il me semble que c'est impossible.
Aucune bûche ne peut remplir le cube central puisqu'il doit rester vide. Dès lors, les deux cubes constitutifs d'une bûche ont toujours des faces visibles, soit 3 soit 5.
Soit x le nombres de bûches à 5 faces visibles et y le nombre de bûches à 3 faces visibles.
5x + 3y = 54
x + y = 13
Le système n'a pas de solutions entières et le dé n'est donc pas constructible.
#13 - 01-07-2012 09:50:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
déd 2
Amusante ta démo looozer 
Vasimolo
#14 - 01-07-2012 10:40:09
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3221
- Lieu: Luxembourg
fés 2
Bonjour,
Cet exercice est impossible à réaliser. En effet, si je colorie mes 26 cubes alternativement en noir et blanc, à l'image d'un damier 3D, en supprimant le cube central blanc, j'aurais 14 cubes noirs pour seulement 12 cubes blancs. Comme mes buchettes seront composées d'un cube noir et d'un cube blanc, je serai en déficit de 2 cubes noirs. Voici une tentative d'illustration, en tranches:
Tr.1 / Tr.2 / Tr.3
N B N / B N B / N B N
B N B / N X N / B N B
N B N / B N B / N B N
Merci et bonne journée.
#15 - 02-07-2012 10:02:30
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
déq 2
C'est une nouvelle version du problème des sept ponts de Königsberg ?
Il n'y a aucune solution .
Supposons que l'on décrive l'arrangement en passant par une chaîne continue d'une buchette à l'autre qui la touche.
Chaque cube au milieu d'une face devrait être une extrémité de la chaîne : il manque donc 4 extrémités  ! !
#16 - 02-07-2012 14:28:35
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Déés 2
Le cube contiendrait 26 dés elementaires ou 13 buchettes.
Il y a 8 coins soit 8 buchettes. Aucune ne permet d'atteindre un centre de face, or il y en a 6. Le cube ne peut etre construit.
The proof of the pudding is in the eating.
#17 - 02-07-2012 15:11:15
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
és 2
Associons une couleur à chacun des 27 "petits cubes" du grand cube.
Je commence par un des coins de la face supérieure en noir et la couleur est alternée de cube en cube.
Ainsi pour la face supérieure, j'ai 5 cubes noirs (les coins et le centre) et 4 blancs (les milieux des côtés).
La face inférieure est identique et la face intermédiaire a elle 4 noirs et 5 blancs.
Sur cette face, le petit cube central est blanc.
Comme celui-ci est enlevé, le cube complet est formé de 14 cubes noirs et 12 cubes blancs.
Comme chaque buchette est composée d'un cube noir et d'un cube blanc, il est impossible de recomposer ce cube privé de son élément central.
On pourrait y arriver pour un cube privé d'un élément de coin ou d'un centre de face.
Pour le 5x5x5 privé de son élément central, il n'y a pas de difficulté à le construire avec des buchettes.
On construit la tranche centrale comme ceci:
Les 2 tranches du haut peuvent se construire de façon identique avec une buchette qui descend par le trou central et idem pour les 2 faces du bas.
Merci pour ce petit rafraichissement de mémoire 
#18 - 02-07-2012 15:27:09
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Dé s2
Si on colore les cubes en noir et blanc alternativement, de façon à ce que les huit cubes des coins soient en noir, on voit qu'il y a 14 cubes noirs et 12 blancs. Or chaque "bûchette" est constituée d'un cube noir et d'un blanc. Aucun espoir que ta construction aboutisse, donc.
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#19 - 02-07-2012 15:35:32
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 102
Dés
Supposons, pour faire plus joli, qu'on veuille constituer le dé creux à l'aide de 26 petits cubes de deux couleurs différentes pour le faire ressembler vu de loin à un petit damier (ou un petit échiquier, selon les goûts), donc de telle manière que deux petits cubes adjacents ne soient jamais de la même couleur.
Si on prend par exemple des petits cubes blancs et noirs et si on commence par mettre un cube noir pour un des coins du dé, on va se retrouver avec tous les cubes "coins" en noir, ainsi que tous les cubes centraux des faces. Les cubes restants seront blancs.
Et là, si on compte les cubes, on se retrouve avec 14 cubes noirs et 12 cubes blancs.
Comme on est parti du principe que notre dé n'avait pas deux petits cubes adjacents de même couleur, chaque buchette étant un ensemble de deux cubes adjacents, elle sera constituée d'un cube noir et d'un cube blanc.
Hum... on commence à sentir le problème, parce que vu comme ça, on pourra s'y prendre de toutes la manières qu'on veut, avec nos 13 buchettes bicolores, on va se retrouver à la fin avec autant de cubes blancs que noirs, et on ne pourra jamais obtenir 14 cubes noirs et 12 cubes blancs.
Il est donc impossible de placer les buchettes pour réaliser le dé creux !
#20 - 02-07-2012 15:41:59
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 102
Dé s2
Au fait, pour un cube creux 5x5x5, c'est le même raisonnement, si on veut le faire bicolore alterné, on se retrouve avec 50 cubes noirs et 48 cubes blancs (si on démarre par du noir pour un des coins du dé).
Une fois de plus, on n'a pas autant de noirs que de blancs, il est donc impossible de placer des buchettes bicolores pour réaliser le dé creux 5x5x5 !
Idem pour tout dé NxNxN avec N impair...
#21 - 02-07-2012 17:02:24
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3221
- Lieu: Luxembourg
Dsé 2
Complément à mon post #14 ci-dessus: généralisation du problème
Je m'aperçois que l'exercice est impossible à réaliser pour tout dé n x n x n tel que n = 4k - 1. En effet, si je colorie mes cubes d'angle en noir (et tous les autres cubes alternativement en noir et blanc, comme un damier 3D), j'aurai, y compris le cube central, (n³+1)/2 cubes noirs et (n³-1)/2 cubes blancs. Si je veux "deséquilibrer" le nombre de cubes, il faut que le cube central soit blanc (et surtout pas noir), ce qui donne n = 4k - 1. A l'inverse, si n est pair ou si n = 4k - 3, alors l'exercice est réalisable.
#22 - 03-07-2012 16:30:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Dés
Beaucoup de bonnes réponses 
L'idée la plus simple , donnée à plusieurs reprises , est de colorier les petits cubes alternativement en noir et blanc . Chaque buchette est constituée d'un cube de chaque couleur . La couleur du cube central est minoritaire ( 13 pour 14 ) donc le cube qui ne sera pas recouvert par la buchette n'a pas la couleur du cube central et ce n'est donc pas lui .
Le même raisonnement s'applique à tout dé de côté impair .
Merci pour la participation 
Vasimolo
#23 - 03-07-2012 16:51:15
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3221
- Lieu: Luxembourg
éDs 2
@Vasimolo: Je ne suis pas d'accord: le même raisonnement ne s'applique pas à tout dé de côté impair, mais certains seulement (voir mon post #21 d'hier). Voici l'exemple du dé 5x5x5 qu'on pourrait réaliser avec 62 bûchettes comme suit:
Tranche 1 / Tranche 2 / Tranche 3 / Tranche 4 / Tranche 5
01 02 03 04 05 / 01 02 03 04 05 / 26 27 28 29 30 / 38 39 40 41 42 / 38 39 40 41 42
06 07 08 09 10 / 06 07 08 09 10 / 26 27 28 29 30 / 43 44 45 46 47 / 43 44 45 46 47
11 12 13 14 15 / 11 12 13 14 15 / 31 31 xx 32 32 / 48 49 50 51 52 / 48 49 50 51 52
16 17 18 19 20 / 16 17 18 19 20 / 33 34 35 36 37 / 53 54 55 56 57 / 53 54 55 56 57
21 22 23 24 25 / 21 22 23 24 25 / 33 34 35 36 37 / 58 59 60 61 62 / 58 59 60 61 62
#24 - 03-07-2012 16:54:36
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,985E+3
Dsé 2
Il y a comme une incompréhension...
Dans ma tête, l'enveloppe 5x5x5 etait totalement creuse. donc pas de cube 3x3x3 au centre.
#25 - 03-07-2012 17:00:15
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Dé s2
Effectivement. Là, c'est une vraie preuve, mais on peut facilement invalider l'argument des bûchettes bicolores pour tout cube de dimensions 4n+1, cas dans lequel on a un nombre pair de "tranches" de chaque côté de la "tranche" centrale (on peut alors les rassembler par paires, une tranche aux coins noirs avec son "négatif"), et une tranche centrale qu'on peut décomposer en un + central (lequel a 2n cubes sur chacune de ses quatre branches) et quatre carrés de côté 2n. Donc, même nombre de noirs que de blancs, quoi qu'il arrive.
L'argument bicolore s'applique uniquement à un cube de dimensions 4n+3.
Addendum : ...sauf, viens-je de tilter, si on ne garde à chaque fois que l'enveloppe extérieure (on enlève le cube de côté k-2 au centre du cube de côté k), auquel cas l'argument est totalement valide.
Pas évident de généraliser proprement en partant seulement du plus petit exemple 
PS : arf, grillé par Gwen 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







