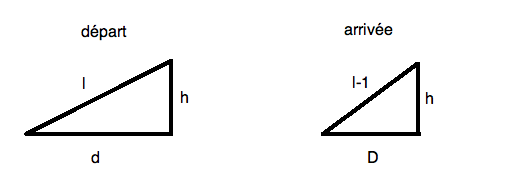Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 07-01-2013 12:17:59
Bateau sru l'eauPour fêter 2013, voici une petite énigme qualitative que j’ai trouvée amusante:
#0 Pub#2 - 07-01-2013 13:18:26
bateau sur k'eauOn s'en sort avec un peu de pythagore: #3 - 07-01-2013 15:46:47
Bateau sur l'aeuAu départ, on a un triangle rectangle de côtés a, b et c; a étant la distance horizontale de la pointe du bâteau au quai, b étant l'altitude entre le bâteau et mes mains et c étant la longueur de la corde. On aura: a²+b²=c². #4 - 07-01-2013 16:45:33#5 - 07-01-2013 18:32:04
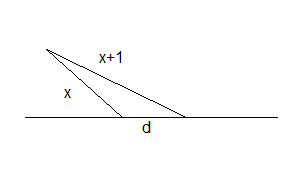
Baateau sur l'eauQuand on prend les 2 positions successives de la corde et la distance parcourue par le bateau, on obtient un triangle dont le plus grand côté est X+1 et dont un des côtés mesure X . #6 - 07-01-2013 18:35:34
BBateau sur l'eauBonnes réponses de tout le monde jusqu'à maintenant (plus ou moins détaillées). #7 - 07-01-2013 21:45:20
batezu sur l'eauÉtrangement, il a avancé de plus d'un mètre... #8 - 08-01-2013 06:32:49
Bateau sur l'eaSi h est la hauteur du quai au dessus de l'eau et x la longueur de la corde, les distances d1 et d2 entre quai et bateau dans les 2 configurations sont: #9 - 08-01-2013 11:47:14
Bateau sur l''eauBon ben moi aussi je vois un triangle rectangle où la corde serait l'hypoténuse donc forcément le côté le plus long donc le bateau avance de moins d'un mètre. #10 - 08-01-2013 11:58:00
Batea sur l'eauSi on note 'a' la longueur de la corde après avoir tiré et x le déplacement du point d'attache de la barque à la corde, alors l'inégalité triangulaire donne 1+a < x+a #11 - 09-01-2013 10:50:24#12 - 11-01-2013 15:29:26
Bateua sur l'eauRien à rajouter, ma solution utilise aussi l'inégalité triangulaire: #13 - 11-01-2013 17:36:48
BBateau sur l'eauPar contre, il faut vraiment tirer très fort !! Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.