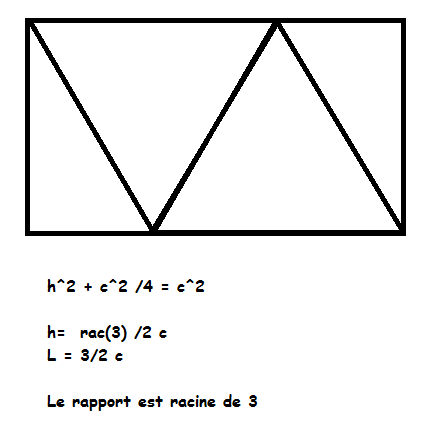Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 29-05-2014 12:24:32
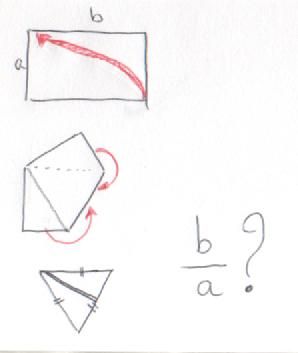
Pligaeil m'est venu une question en pliant un billet de 5 euros qui répond presque à la question :
#0 Pub#2 - 29-05-2014 12:56:59#3 - 29-05-2014 12:59:57
liagec'est la bonne réponse, mais je ne savais pas comment la noter . #4 - 29-05-2014 13:04:19#5 - 29-05-2014 14:01:54
pmiageSi je ne m'abuse, c'est tout bête. Soit le triangle équilatéral de côté "c", alors : #6 - 29-05-2014 14:12:28
pliafeOK , c'est la bonne réponse, et bien vu . #7 - 29-05-2014 14:41:23
PliaegBonjour, Il y a sûrement plus simple. #8 - 29-05-2014 14:44:27
PlageOK #9 - 29-05-2014 22:08:59
plizgeSur la deuxième figure le triangle rectangle formé par le pliage à un trois angles de respectivement 90°, 60° et 30° "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #10 - 29-05-2014 22:16:20
pliafec'est une façon de voir . Bravo #11 - 30-05-2014 06:22:23#12 - 30-05-2014 08:16:18
pliahe(1+1/2)/(V3/2)=V3=env.1.732 #13 - 30-05-2014 08:25:17#14 - 30-05-2014 12:22:23#15 - 30-05-2014 17:16:37
pliaheBonjour #16 - 30-05-2014 17:47:08#17 - 30-05-2014 19:57:19#18 - 31-05-2014 23:03:07
oliageDe toute façon le dessin je l'ai refait moi-même donc qu'importe, mais ma méthode n'est pas directe, du moins j'ai fais pas mal de calcul j'attends de voir plus simple "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #19 - 01-06-2014 14:40:23
pliagrSoit c le coté du triangle. Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.