Bonjour,
Ce Gateau 69 me turlupine, et ce n'est pas une contrepèterie ...
... quoi que ...  )
)
Pour comprendre je suis reparti de l'exemple de la figure à 10 points, avant d'essayer de généraliser ...
Tout d'abord, on rappelle que [latex]\frac{n(n-1)}{2}[/latex] segments relient [latex]n[/latex] points distincts.
Ensuite, que la longueur d'un segment est proportionnelle au nombre d'arcs de cercle qui les séparent.
Dit autrement, si [latex]\alpha[/latex] est l'angle d'un secteur séparant deux points consécutifs, la longueur d'un segment séparant [latex]k+1[/latex] points consécutifs sur le périmètre du cercle est [latex]2R sin(\frac{k\alpha}{2})[/latex] avec [latex]R[/latex] rayon du cercle
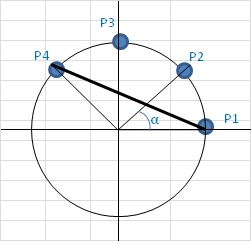
On a donc bien une relation entre la position relative des points et la longueur du segment qui les relie.
Je repars de la figure de l'énoncé avec les conventions suivantes :
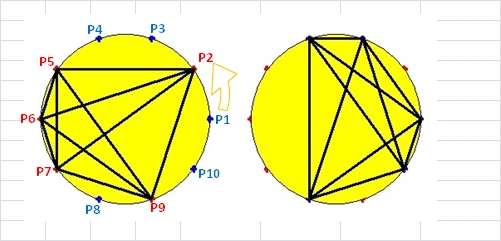
puis je dresse le tableau suivant (zoomable) :
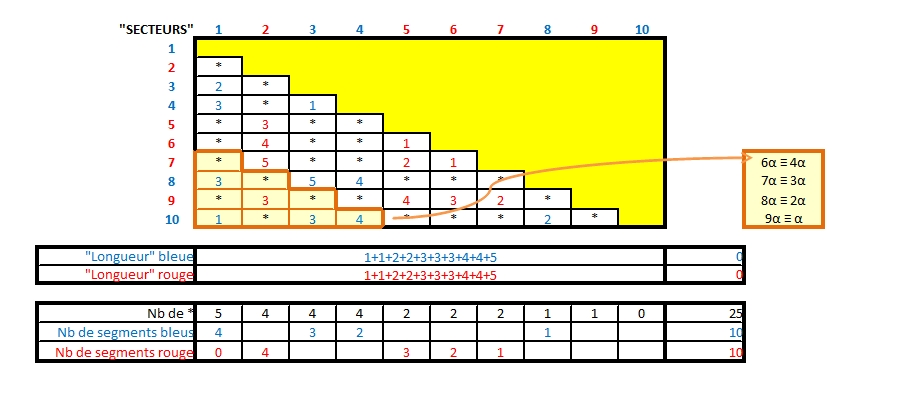
Ce que j'appelle "secteurs" est le plus petit nombre de parts de gâteau séparant deux points, on a vu en introduction que la longueur du trait de chocolat est en fonction.
La notion de "plus petit" est introduite ici dans la zone "orangée" pour introduire le fait que [latex]sin(\frac{\alpha}{2})=sin(\frac{2\pi-\alpha}{2})[/latex]
Jusqu'à 6, c'est la différence d'indice entre deux points.
Exemple entre P6 et P2 il y a quatre secteurs.
Après 6, par exemple entre P10 et P1 il y a 9 secteurs, congruents à 1 seul.
On a dans les deux cas 10 segments [latex]\frac{5(5-1)}{2}[/latex][/latex] alors que relier les 10 points demandent 45 segments.
Le choix "rouge/bleu" laisse donc 25 segments non tracés, d'où les * dans le tableau.
Avec cette convention, je retrouve bien que le chemin reliant les 5 points "bleus" est égal au chemin reliant les 5 points "rouges".
La sommation donne un résultat identique, il me semble que c'est un peu hasardeux de continuer sur cette voie avec la fonction sinus qui intervient derrière cette convention, mais bon, on recherche plutôt les positions relatives des points choisis et des points exclus en fait ... (modulo leur répartition sur le périmètre d'un cercle)
En tous cas la décomposition du chemin est identique.
Il y a autant de portions d'égale longueur dans chaque cas.
............................
Bon si je m'arrête là, cela fait beaucoup de recherches et de formules [latex]LaTex[/latex] pour compter les traits de la figure de l'énoncé.
Je vais revenir en espérant trouver la généralisation !
J'ai essayé aussi en essayant de modéliser les points choisis / exclus en binaire, par exemple le choix de l'énoncé avec P1 selon convention du cercle "trigo" serait codé 1011000101 ou son complément 0100111010 selon qu'un "bit à 1" est rouge ou bleu.
A+

 Accueil
Accueil
 Forum
Forum









