bonjour.

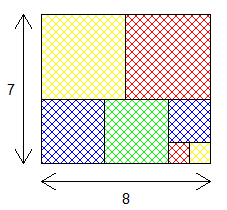
@vasimolo , ton exemple ne serait pas plutôt un rectangle 8 x 7 ?

Ton dessin est faux, Vasimolo, je crois.

En utilisant la récursivité, on arrive à l'algorithme suivant:

http://www.prise2tete.fr/upload/kossi_t … Carres.png

Quelques exemples:

(8,7)=7

(127,7)=24

(17,6)=7

(100,57)=11

(259,101)=13

Vasimolo, il subsiste un défaut sur ton dessin.

Sinon, je n'ai pas grand chose, juste une conjecture.

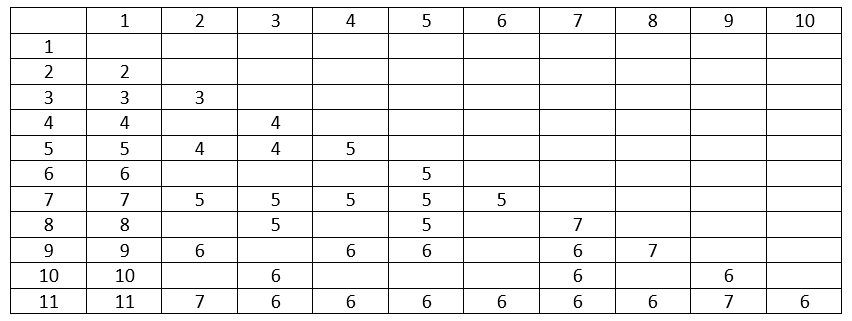
On considère un rectangle (a,b) premiers entre eux et tel que a<b<2a. Tout rectangle dont b>2a est ramené au cas énoncé en ôtant autant de fois que nécessaire le carré a. Si (a,b) ne sont pas premiers entre eux, on divise par leur PGCD pour se ramener au cas énoncé.

Conjecture:
Si (a,b) sont 2 nombres successifs de Fibonacci, alors le nombre de carrés est le rang de a dans la suite de Fibonacci.
Rappel des nb de Fibo: 1,1,2,3,5,8,13,21....
Pour le rectangle (3,5), donc 4 carrés.
Pour le rectangle (13,21): 6 carrés.
etc...
Autrement dit, il est impossible de couvrir ces rectangles avec moins de carrés.

Pour les autres (a,b) qui ne sont pas des nombres de Fibonacci, conjecture:
Si (Fn,F(n+1))<(a,b) alors le nombre de carrés nécessaires pour couvrir (a,b) est supérieur ou égal au nombre de carrés nécessaires pour couvrir (Fn, F(n+1)). 

Les premiers (a,b) et le nombre de carrés associés:
(1,2) 2 Fibo
(2,3) 3 Fibo
(3,4) 4
(3,5) 4 Fibo
(4,5) 5
(4,7) 5
(5,6) 5
(5,7) 5
(5,8) 5 Fibo
(5,9) 6
(6,7) 5
(6,11) 6
(7,8) 7
(7,9) 6
(7,10) 6
(7,11) 6
(7,12) 6
(7,13) 6
(8,9) 7
(8,11) 6
(8,13) 6 Fibo
(8,15) 8
(9,10) 6
(9,11) 7
(9,13) 7
(9,14) 7
(9,16) 7
(9,17) 8
((10,11) 6
(10,13) 7
(10,17) 7
(10,19) 7
(11,12) 8
(11,13) 8
(11,14) 7
(11,15) 7
(11,16) 7
(11,17) 7
(11,18) 7
(11,19) 7
(11,20) 8
(12,13) 8
(12,17) 7
(12,19) 7
(12,23) 9

Attention Vasimolo, prendre le carré de la largeur ne conduit pas tjs au min. Voir (6,7)--->(6,6)+(1,6) donne 7 alors que (6,4)+(6,3) donne 5.
Plus généralement, pour les couples du genre (2n, 2n+-1), on ramène normalement à (n,2n)+(n+-1,2n)=2+(n+-1,2n).
Pour les premiers jumeaux (p,p+2), je n'ai pas trouvé mieux que (p,p)+(2,p).

Oui c'est vrai. Mea Culpa à cause d'une interprétation hâtive. En fait, je te rejoins sur tes commentaires. En revanche, il me semble de plus en plus incertain qu'il puisse exister une règle de calcul générale.

Je suis malheureusement d'accord avec toi les quasi-carrés posent vraiment de gros problèmes . Bizarrement je n'ai pas trouvé de littérature sur ce problème pourtant assez "naturel" .

Il reste quand même l'étude de cas particuliers qui peuvent être très intéressants .

Par exemple : Une preuve que N(km,kn)=N(m,n) ou un contre-exemple ?

Vasimolo

Salut,

Jetez un coup d`oeil ici :

http://demonstrations.wolfram.com/Minim … ectangles/

ou la :

http://ac.els-cdn.com/S0097316596901041 … 279c9fc441

Un article assez long.


Je viens de voir cela sur un autre forum.