Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 18-08-2010 16:41:47
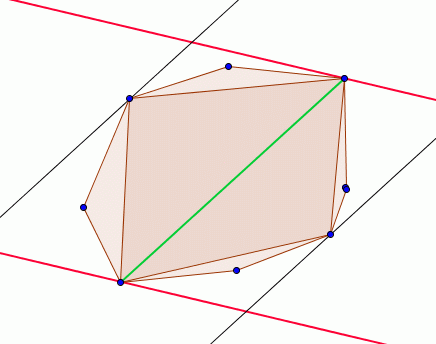
Gâetau 27Un peu dans le même style que le gâteau 25 du SingeMalicieux mais en plus difficile
#0 Pub#2 - 20-08-2010 12:08:07
Gâteu 27Vu le dessin illustrant le problème, j'ai supposé que la règle de découpe du quadrilatère consiste à choisir 4 sommets du n-polygone initial... #3 - 21-08-2010 11:54:55#4 - 21-08-2010 23:33:49#5 - 22-08-2010 21:28:52
Gâteaau 27
Celui qui fuit les casse-tête ne vaut pas un clou. #6 - 22-08-2010 23:55:32
Gtâeau 27Bravo scrablor #7 - 23-08-2010 07:17:55
GGâteau 27Je m'etais egare sur les terres du theorme de Pick puis sur celle de la triangulation... The proof of the pudding is in the eating. #8 - 23-08-2010 16:01:34
gâteai 27Pareil : ce n'est pas que je n'ai pas aimé ce gâteau, c'est que je ne voyais pas par où l'entamer... Ca a l'air si simple que je m'en veux de ne pas avoir eu l'idée... Bravo Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #9 - 23-08-2010 16:50:49
gâteay 27En fait mais si la fin est la même , la méthode de scrablor n'est pas tout à fait celle que j'avais employée et commencée à décrire dans mon indice . Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.