 |
#1 - 06-04-2015 11:25:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 06-04-2015 16:19:48
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâtteau 96
Je dirais Spoiler : [Afficher le message] 10x29 ... j'ai bon ?
3 petites remarques :
* il peut être constructif de ne pas être constructif.
* il n'y a pas unicité de la solution.
* mesurer l'image de Vasimolo fournit un gros indice 
#3 - 06-04-2015 17:27:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteu 96
@Ebichu : c'est la bonne réponse 
Tu es sûr que la solution n'est pas unique ? La solution est la taille du gâteau , pas son découpage .
Vasimolo
#4 - 06-04-2015 18:25:35
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâeau 96
En effet, "il n'y a pas unicité du découpage" est une formulation moins ambiguë 
#5 - 07-04-2015 10:50:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
GGâteau 96
Il n'y a pas foule sur le problème , je donne un petit indice 
Spoiler : [Afficher le message] Commencer par encadrer la taille des carrés pouvant être construits avec cinq rectangles de côtés : 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 et 10 .
Bon courage !
Vasimolo
#6 - 07-04-2015 18:40:46
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
GGâteau 96
Je pense que c'est maintenant que j'ai compris le problème. Par la phrase Les parts portant une bougie bleue ont des côtés qui décrivent tous les entiers de 1 à 10
, j'avais compris qu'il faille faire un découpage qui décrit graphiquement l'écriture des entiers 1 à 10. Il fallait comprendre la mesure des côtés des rectangles. Ok, je m'y mets 
#7 - 07-04-2015 18:59:45
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Gâteauu 96
10+18+24+28+30 = 110
90+56+30+12+2= 196
Les carrés font donc 121 144 169 ou 196
Soit 6 couples : dont le total fait :
121 + 144 = 265 = 5 x 53
121 + 169 = 290 = 2 x 5 x 29
121 + 196 = 317 = 317 x 1
144 + 169 = 313 = 313 x 1
144 + 196 = 339 = 3 x 113
169 + 196 = 365 = 5 x 73
Seul 290 me parait crédible avec un rectangle de 10 x 29.
Est-il possible, j'ai un peu la flemme de chercher 
#8 - 07-04-2015 19:28:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âGteau 96
C'est ça Gwen , il suffit d'essayer pour conclure 
Vasimolo
#9 - 07-04-2015 21:52:46
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gâetau 96
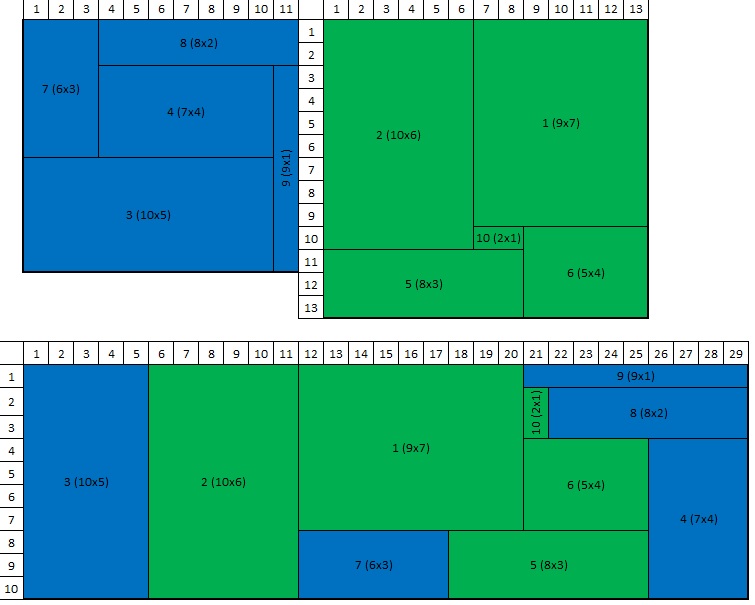
J'ai trouvé 5 ensembles de 5 rectangles dont les côtés vont de 1 à 10 et la somme des aires donnent des carrés parfaits (121, 144 ou 169). Ce pendant, je n'ai arrivé à regrouper que 2 de ces 5 ensembles en carré (figure géométrique). Les rectangles de ces 2 groupes sont regroupés en un rectangle de dimensions 29x10 qui sont les dimensions du gâteau.
Voici le résultat:

#10 - 07-04-2015 22:37:56
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gtâeau 96
Démonstration de l'unicité de la réponse:
5 rectangles dont les côtés vont de 1 à 10, notons SA la somme des aires de ces 5 rectangles.
SA est majorée par 10*9+8*7+6*5+4*3+2*1=190 (les plus grands rectangles qu'il est possible d'avoir en même temps) et est minorée par 10*1+9*2+8*3+7*4+6*5=110 (les plus petits rectangles qu'il est possible d'avoir en même temps).
Entre 110 et 190, il n'y a que 3 carrés parfaits qui sont 121, 144 et 169 donc il n'existe que 3 dimensions possibles pour les carrés bleus et verts.
En combinant 2 à 2 ces nombres carrés parfaits, on a:
** 1er cas: 121+144=265=53*5. Pour pouvoir avoir ce gâteau, il faut que la largeur de tous les rectangles soit inférieure ou égale à 5 or dans ce cas le plus gros gâteau qu'il est possible d'avoir est (10*5+9*4+8*3+7*2+6*1)*2=260<265 donc notre gâteau n'est pas formé de 2 carrés 11x11 et 12x12.
** 2è cas: 144+169=313 qui est nombre premier donc tous les rectangles auraient une larguer égale à 1. Impossible.
** 3è cas: 121+169=290=29*10 ou =145*2 ou = 58*5. Les 2 dimensions 145*2 et 58*5 sont impossibles pour des raisons évidentes (voir le 1er cas).
L'unique solution possible est donc 29x10 si elle existe et le poste précédent montre qu'elle existe.
CQFD.
#11 - 07-04-2015 23:06:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteai 96
Bravo Kossi 
Et joliment illustré .
Il n'était pas si difficile ce gâteau 
Vasimolo
#12 - 08-04-2015 14:36:43
- dbab3000
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 111
Gâtau 96
En sachant que chaque 5 parts sont égaux alors ils ont le même aire ce qui signifie que les aires des carrés sont divisibles par 5,on a:
Un carré de côté 5 qui a un aire de 25=5×(5×1) qui peut être formé par 5 rectangles (bleus) de dimension 5×1 car 5 peut s'écrire sous la forme 5=5a et 5=1b tel que a et b sont des entiers.
Un carré de côté 10 qui a un aire de 100=5×(2×10) ou 100=5×(5×4) mais pour le deuxième cas on ne peut pas former un carré avec des rectangles de dimension 5×4 car 10 ne peut pas s'écrire sous la forme 10=4a+5b ou 10=4a par contre elle peut s'écrire sous la forme 10=2a et 10=10b alors le deuxième carré est formé par des rectangles (verts) de dimensions 2×10.
On a 100+25=125 c'est l'aire du rectangle qu'on veut trouver et 125=1×125=5×25 le rectangle ne peut pas avoir une dimension de 1×125 avec les parts que nous avons donc sa dimension est 5×25 .
Bonne journée.
#13 - 08-04-2015 16:14:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 9
@dbab : je crois que tu n'as pas bien compris le problème 
Vasimolo
#14 - 08-04-2015 16:39:06
- dbab3000
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 111
Gâteauu 96
Est ce que chaque 5 parts sont égaux? A mon avis,c'est l'information qui a faussé mon raisonnement.
#15 - 08-04-2015 16:55:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâetau 96
En effet tu n'es pas sur la bonne piste 
Le gâteau est coupé en deux fois cinq rectangles dont les dimensions sont 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 et 10 dans chacun des deux groupes .
On pourrait imaginer par exemple un rectangle découpé en rectangles :
1X5 ; 2X4 ; 3X7 ; 6X9 ; 8X10 et 1X4 ; 2X5 ; 3X6 ; 7X10 ; 8X9 .
Chacun des deux paquets de cinq rectangles pouvant constituer un carré de taille différente .
Vasimolo
#16 - 08-04-2015 23:36:00
- dbab3000
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 111
Gâetau 96
Merci Vasimolo pour l'explication,j'étais vraiment sur la mauvaise piste, je vais rectifier, avec 5 parts bleus ou verts le plus petit aire est 10×1+9×2+8×3+7×4+6×5=110 et le plus grand aire est 10×9+8×7+6×5+4×3+2×1=190 alors les seuls carrés qu'on peut former ont un côté 11,12 et 13 avec des aires respectivement 121,144 et 169,on a 3 cas:
-L'aire des deux carrés bleus et verts sont respectivement 144 et 169 alors l'aire du gâteau est 144+169=313 mais 313 est un nombre premier alors il ne peut s'écrire que sous la forme 313=313×1 le gâteau ne peut pas avoir cette dimension c'est un cas impossible.
-L'aire des deux carrés bleus et verts sont respectivement 121 et 144 alors l'aire du gâteau est 121+144=265, 265 peut s'écrire sous la forme 265=265×1=5×53
265×1 ne peut pas être sa dimension et pour 5×53 en supposant que le gâteau a cette dimension toutes les parts rectangulaires doivent avoir un couple longueur et largeur (L,l) tel que L>5 et l≤5 cependant le plus grand aire qu'on peut former avec ses rectangles est 5×10+4×9+3×8+2×7+1×6=130 alors on ne peut pas former un carré qui a un aire de 144 c'est un cas impossible.
-Les deux carrés bleus et verts ont respectivement un aire 121 et 169 alors l'aire du gâteau est 121+169=290 qui peut s'écrire sous la forme 290=29×10 donc la dimension du gâteau est 29×10. J'espère que ce n'est pas faux cette fois ci ^^
Bonne nuit
#17 - 09-04-2015 17:58:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 996
Bravo à wen et Dbab qui ont montré que la seule possibilité était 29X10 et bien sûr à Kossi qui a prouvé par l'exemple que c'était possible .
En fait 11 et 13 sont les seuls carrés réalisables , 12 vérifie bien les inégalités mais ne peut pas être pavé avec les 5 rectangles voulus .
Vasimolo
#18 - 09-04-2015 23:36:32
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâetau 96
Avec un programme, sur les 9x7x5x3=945 façons de regrouper par paires les entiers de 1 à 10, il y en a 14 qui permettent d'obtenir une aire de 121, et 12 qui permettent d'obtenir une aire de 169.
Parmi ces 14 et 12 façons, je n'en ai trouvé que 2 de chaque sorte (par une méthode manuelle, il est rapide de vérifier si 5 rectangles s'organisent en carré) qui permettent de reconstituer des carrés de 11x11 ou 13x13 :
1*6 + 2*10 + 3*9 + 4*7 + 5*8 = 121 (A)
1*9 + 2*8 + 3*6 + 4*7 + 5*10 = 121 (B)
1*2 + 3*7 + 4*6 + 5*10 + 8*9 = 169 (C)
1*2 + 3*8 + 4*5 + 6*10 + 7*9 = 169 (D)
J'arrive à assembler (B) et (D) (comme kossi), ou bien (A) et (D) pour former le gâteau de taille 29x10.
Par contre, je n'arrive pas à assembler (A) et (C), ni (B) et (C), sans pour autant avoir de preuve que ce soit impossible... quelqu'un a-t-il plus de réussite que moi ?
|
 |

 Accueil
Accueil
 Forum
Forum








