|
#1 - 18-04-2015 20:27:21
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
un gateau parfaitelent divisé
Bonjour 
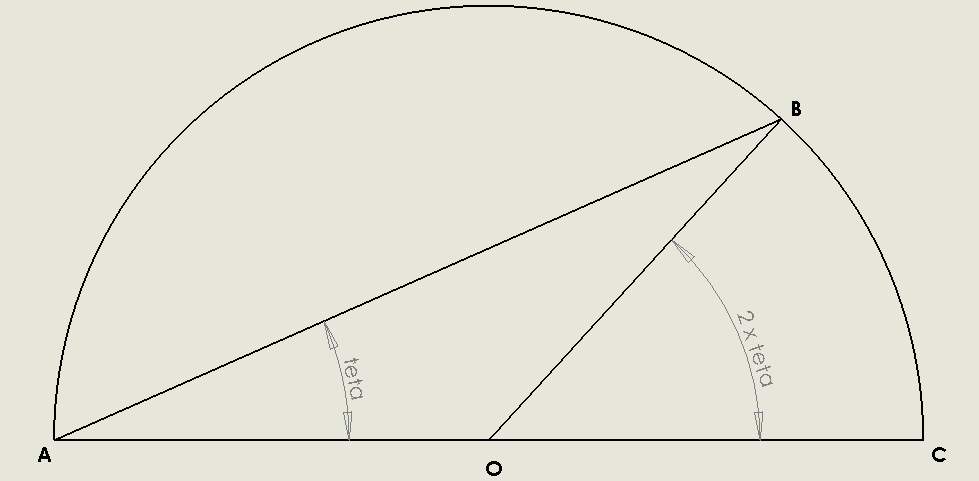
Hier j'ai cuisiné un gâteau en forme de demi disque parfait. J'y ai d'ailleurs mis un glaçage vert et bleu. J'ai utilisé la même quantité de glaçage des deux couleurs, donc ils occupent la même surface. La ligne de démarcation entre les deux glaçages est nette, rectiligne, et part d'un coin.
Mais combien vaut l'angle Thêta?

On donnera une réponse en radians, à un millième près (exemple 0.123)
Bonne chance! 
Un promath- actif dans un forum actif
#2 - 18-04-2015 23:23:30
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
U gateau parfaitement divisé
#3 - 19-04-2015 09:23:35
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Un gateau parfaitement ivisé
salut.
en posant x = 2.thêta --> x = pi/2 - sin x --> x = 0.8317 et thêta = 0.416 rd
#4 - 19-04-2015 09:59:27
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
un gateau parfaitelent divisé
Deux bonnes réponses !
Sydre, j'ai plus simple que ta methode 
Un promath- actif dans un forum actif
#5 - 19-04-2015 10:22:47
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
un gateau parfzitement divisé


En prenant pi - 2 theta à la place du Théta de wiki :
PI/2 = pi - 2 theta - sin (pi - 2 theta)
PI/2 = 2 theta + sin (2 theta)
0,4158 ni 0,415, ni 0,416 ne sont validés.
#6 - 19-04-2015 11:21:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Un gateau parfaitemeent divisé
Bonjour Promath 
On découpe la partie bleue en deux triangles rectangles d'angle Ô et d'hypoténuse 1 ( le rayon du demi-cercle ) et en un secteur circulaire d'angle 2Ô . Comme elle doit faire un quart du disque on a : Ô+cosÔ.sinÔ=pi/4 .
Le reste c'est pour les machines .
Vasimolo
#7 - 19-04-2015 15:26:37
- papiauche
- Sa Sainteté
- Enigmes résolues : 49
- Messages : 2131
un gateau parfaitement dicisé
Celle-là est dans mes cordes. 
Je remplace théta par a...
En traçant le segment entre le centre du cercle et le point du périmètre à la frontière des deux aires je divise l'aire bleue en un triangle isocèle et un quartier de disque.
Les aires respectives (pour un rayon de 1) sont 2a/2=a et sin(a)cos(a)=1/2sin(2a).
Leur somme doit valoir la moitié de pi/2, soit pi/4
a+1/2sin(2a) = pi/4
Pour une valeur approchée de 0.416 (merci wolfram)
Et hop !
"Je ne lis jamais un livre dont je dois faire la critique. On se laisse tellement influencer." O. Wilde
#8 - 19-04-2015 15:33:22
- fmifmi
- Passionné de Prise2Tete
- Enigmes résolues : 18
- Messages : 87
Un gataeu parfaitement divisé
On considere la surface en bleu qui vaut pi*r²/4
elle est la somme de:
1)un secteur circulaire d' angle 2 teta donc s=teta*r²
2)un triangle isocele dont la surface est r*cos(teta)*r*sin(teta) soit r² sin(2*teta)/2
on obtient l'equation 2*sin(2*(teta)) + 4*teta - pi=0
tableur donne teta= 0,4158
#9 - 19-04-2015 15:52:32
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Un gateau paraitement divisé
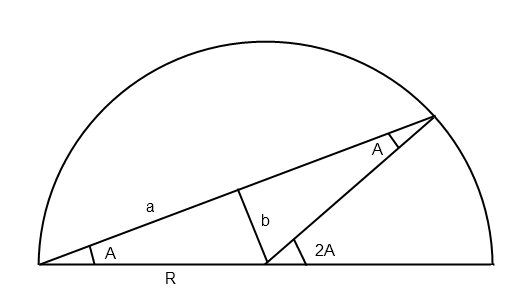
L’angle du camembert de droite vaut: pi - 2.(pi / 2 - A) = 2A
L’aire du camembert de droite vaut donc: A.R²
L’aire des deux triangles rectangles vaut: a.b = R².cosA.sinA = R².sin2A / 2
On a la relation: A.R² + R².sin2A / 2 = pi.R² / 4, ou: 4A + 2.sin2A – pi = 0
On trouve: A = 0,416 rad env., validé par la case-réponse
#10 - 19-04-2015 17:45:10
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Un gateau parfaitment divisé
On rajoute le rayon qui joint le centre au point du cercle situé sur la frontière entre les deux glaçages, en haut à droite.
L'angle entre l'axe et ce rayon vaut 2θ par le théorème de l'angle au centre.
Ce rayon partage le glaçage bleu en deux parties, une portion de disque d'aire θ, et un triangle d'aire sin(2θ).
On en tire l'équation 2θ+sin(2θ)=π/2 qui après résolution numérique donne θ≈0,416.
Joli problème 
#11 - 19-04-2015 18:48:44
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Un gateau pparfaitement divisé
gwen: bonne réponse. Pour la case réponse, relis l'exemple, c'est un point 
Vasimolo: je ne comprends pas ta méthode, tu tombes sur quoi au final?
papiauche, fmifmi, Franky1103, Ebichu : c'est ok 
Un promath- actif dans un forum actif
#12 - 19-04-2015 19:06:22
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
un gateau parfaitzment divisé
Ca va, je me sens moins bête 
#13 - 19-04-2015 19:58:02
- alfalf31
- Amateur de Prise2Tete
- Enigmes résolues : 1
- Messages : 1
un gateau parfaitement dibisé
Hello,bon ce n'est pas la réponse mais voici mon raisonnement.
Ensemble, la partie bleue et verte représente la moitié d’un disque donc, si chaque partie est égale, on doit trouver theta pour que la partie bleue fasse Pi.R²/4.
Si on divise la partie bleue par une ligne qui passe par le centre du disque et qui rejoint l’intersection de la séparation du gâteau avec le contour du gateau, on obtient une section de gâteau de côté R et d’angle (2.Theta) et un triangle isocèle de côté R.
L’aire du triangle est égale à Rcos(theta) . Rsin(theta).
L’aire de la section est (2.Theta).R²/2 = Theta.R²
Donc on doit résoudre
R².sin(Theta).cos(Theta) + Theta.R² = Pi.R²/4.
On élimine les R² et on multiplie par 2 et on regroupe sin et cos
sin(2.Theta) + 2.Theta = Pi/2
Pi/4 = 0.785 est solution de l’équation
J'ai du me gauffrer quelque part 
#14 - 20-04-2015 09:37:39
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
n gateau parfaitement divisé
Relis bien ton raisonnement 
Un promath- actif dans un forum actif
#15 - 20-04-2015 15:16:06
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Un gatteau parfaitement divisé
Soient O le centre, A-B le diamètre et A-P le segment sécant.
On trace le rayon O-P.
En prenant le rayon comme unité, on défini le triangle OPA d'aire
sin (Thêta)*cos (Thêta)
Les deux zones ont pour aires :
Thêta + sin (Thêta)*cos (Thêta) = pi/2 – Thêta - sin (Thêta)*cos (Thêta)
Thêta est racine de l'équation :
Thêta + sin (Thêta)*cos (Thêta) – pi/4 = 0
soit : Thêta = 041586 (0,416 valide la solution)
Merci de me donner ainsi l'occasion de me replonger dans ce genre de calculs.
J'aurais tendance à oublier ce type de manipulations... 
#16 - 20-04-2015 15:22:35
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Un gateau parfaiteement divisé
Salut à tous,
En donnant au rayon la valeur 1, en appelant x l'angle au centre correspondant à la corde tracée et en demandant que l'aire du demi-disque soit double de celle du segment de disque, j'obtiens l'équation x - sin (x) = Pi/2
WA me donne 2.30988 comme solution de cette équation bien pourrie.
J'en déduis le valeur arrondie de theta : (Pi - x) / 2 = 0.416
Merci, Promath- !
#17 - 20-04-2015 18:26:03
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Un gateau parfaitement diisé
Exact! C'est marrant je compte 3 équations différentes mais qui se ressemeblent et arrivent au même résultat
Un promath- actif dans un forum actif
#18 - 20-04-2015 18:39:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Un gatea parfaitement divisé
L'angle que tu cherches est la moitié de la solution de l'équation : x+sin(x)=pi/2 .
Vasimolo
#19 - 20-04-2015 21:58:48
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
un gateau parfaitemebt divisé
La relation entre teta et 2*teta étant établie (relation des angles inscrits)
aire(ABO)=0.5*R^2*sin(pi-2*teta)=0.5*R^2*sin(2*teta)
aire(OBC)=teta*R^2
on déduit 0.5*R^2*sin(2*teta)+teta*R^2=(0.5*pi*R^2)/2
soit sin(2*teta)+2*teta=pi/2
Numériquement teta vaut approximativement 0.4158555968 radian
#20 - 21-04-2015 00:06:38
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Un gateau parfaiitement divisé
Salut !
Pour aller vite :
1/L'angle au centre vaut 2*téta
2/L'aire de la portion de disque MOB vaut Pi*R²*2*téta/2Pi=R²*téta
3/BM=2Rsin(téta), donc h=Rsin(téta)
4/L'aire du triangle AOM vaut : AM*h/2
=2Rcos(téta)*Rsin(téta)/2
=R²sin(téta)cos(téta)
=R²sin(2téta)/2
5/L'aire de la portion de disque AOM vaut R²(Pi/2-téta)
6/L'aire verte vaut la différence des 5/ et 4/ : R²[Pi/2-téta-sin(2téta)/2]
7/L'aire bleue (foncée+claire) vaut la somme de 4/ et 2/ : R²[téta+sin(2téta)/2]
8/ on a : 6/ = 7/
Pi/2-téta-sin(2téta)/2=téta+sin(2téta)/2
2*téta+sin(2téta)=Pi/2
La table de ma calculatrice me donne 0.416, validé par la case réponse !
Si j'ai le temps je ferai un dessin.
EDIT : Le voici :
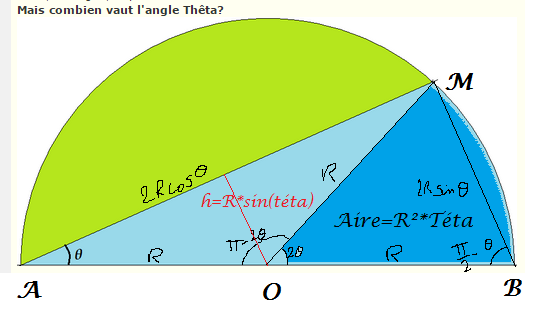
#21 - 21-04-2015 12:05:41
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Un gateau parfaitement diivisé
Vasimolo, kossi_tg, golgot : c'était l'équation que j'avais résolue. Bravo! 
Edit: Vasimolo: petite erreur d'étourderie je pense
Un promath- actif dans un forum actif
#22 - 21-04-2015 13:52:47
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
un gateau parfaiyement divisé
Bonjour,
Voici ma copie :
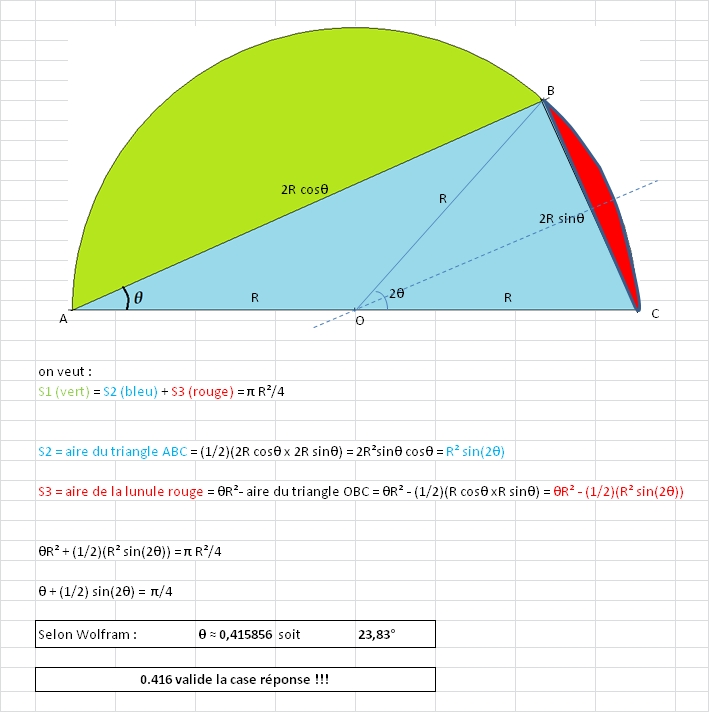
Merci pour cette énigme pâtissière à ma portée ...
(et merci Wolfram !)
A+
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#23 - 21-04-2015 15:38:39
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
un gateau parfaitzment divisé
Très bien! Et s'il n'y avait pas wolfram?
Un promath- actif dans un forum actif
#24 - 21-04-2015 17:24:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Un gateau pparfaitement divisé
Je ne vois pas d'erreur mais si tu le dis 
Vasimolo
#25 - 21-04-2015 17:39:52
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Un gateau parfaiteent divisé
J'avais mal lu ta réponse, je n'avais pas vu le mot "moitié"
Un promath- actif dans un forum actif
|
 |

 Accueil
Accueil
 Forum
Forum