|
#1 - 02-01-2015 15:35:25
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 02-01-2015 16:02:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
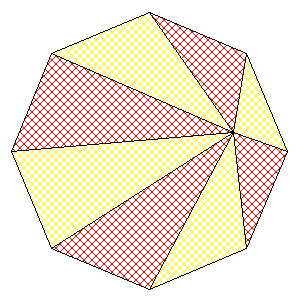
Gâteau 877
Une remarque immédiate: les parts rouges d'une part, jaunes d'autre part, ont la même surface !
#3 - 02-01-2015 16:11:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteu 87
Je n'arrive pas à ouvrir les images du gâteau 2, comment les parts sont elles prises ? Parmi les 2 disponibles (de part et d'autre du vide) ou n'importe lesquelles ?
#4 - 02-01-2015 16:19:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtrau 87
En effet , certaines images du gâteau 2 ont disparu , mais il n'y a pas d'entourloupe , un enfant prend les parts au citron et l'autre celles à la fraise .
Vasimolo
#5 - 02-01-2015 16:23:23
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Gâtea u87
Même surface.
Les triangles issus de face opposées ont la même base pour la même somme des hauteurs.
#6 - 02-01-2015 16:31:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
GGâteau 87
Bien vu Gwen 
Vasimolo
#7 - 02-01-2015 16:45:06
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
hâteau 87
Avec une petite nuance si n/2 est impair, on utilise alors :
Dans un polygone régulier, la somme des distances d'un point intérieur au polygone aux côtés2 du polygone est indépendante de la position du point.
Il suffit alors pour le prouver de tracer les deux triangles identiques utilisant 3 faces non consécutives pour un hexagone, les deux pentagones identiques utilisant 5 faces non consécutives pour un décagone ...
#8 - 02-01-2015 17:03:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 877
Oui Gwen , la propriété en question se justifiant aisément en observant les aires .
Vasimolo
#9 - 02-01-2015 17:26:30
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
hâteau 87
Il apparaît clairement que si on prend sur une diagonale longue, les quantités sont égales. Pour commencer, penchons nous sur le carré. Si on prend sur un côté on voit que les portions sont égales. Dans le cas général c'est aussi valable. Sufit de regarder les triangles qui sont opposés les uns aux autres à gauche et à droite du côté sur lequel se trouve le point de coupe. Idem pour les segments reliant les milieux de côtés opposés
Voyons à l'intérieur du carré. On note x,y les coordonnées du point, avec 0,0 et a,a les coordonnées du carré. Quelque soit x, on remarque que les triangles opposés additionnés ont la même aire. Idem pour y. Ok, c'est statué.
Voyons dans le cas général. On note A1.... A2n les côtés du polygone. On note Ta1 le triangle de A1
On travaille sur A1 pour le moment. Si on déplace le point parallèlement au côté, on remarque que l'aire de Ta1 + Ta(n+1) est constante. Idem pour un déplacement perpendiculaire, car la somme des hauteurs ne varie pas. On généralise à tous les côtés. Ainsi, quelque soit la place du point, la somme de deux triangles opposés est constante. Or, celle-ci est égale à 1/n (position centrale)
Ainsi on a deux cas: si n est pair, l'air est la même pour les deux types de parts.
Sinon... il faudrait que la somme des distances du point aux côtés A(2k) soit constante... Alors là je sèche...
Un promath- actif dans un forum actif
#10 - 02-01-2015 17:32:35
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteau 877
Alors égalité il me semble.
#11 - 02-01-2015 17:36:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 87
Nodgim , il faut prouver 
Vasimolo
#12 - 02-01-2015 17:56:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtaeu 87
Attention , l'exemple choisi n'est pas représentatif de tous les gâteaux 
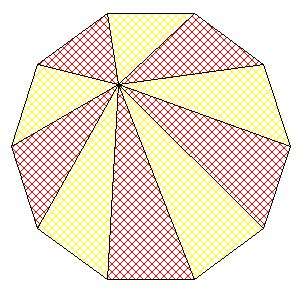
Vasimolo
#13 - 02-01-2015 18:16:56
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâteauu 87
Hello !
Déjà si le polygone à un nombre impair de côtés il y aura toujours un des deux lésé pour la simple et bonne raison qu'on ne peut pas en un coup de couteau, partager en deux ce genre de gâteau en rejoignant deux sommets. Il y en aura donc toujours un avec une part plus grande que l'autre.
Ensuite je dirai qu'aucun des deux n'est gagnant si le gâteau a un nombre pair de sommets. Mais je n'ai pas encore trouver le bon argument, s'il existe, de symétrie.
Affaire à suivre...
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#14 - 02-01-2015 18:43:11
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gâteau 78
Normalement c'est bon car la sistance d'un point aux côtés d'un polygone ne varie jamais!
Donc les parts ont la même aire!
Un promath- actif dans un forum actif
#15 - 02-01-2015 18:44:39
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâtea 87
salut
et tous mes bons vœux pour les années à venir .
pour les gâteaux , les deux enfants se partagent un gateau en polygone régulier à 4n côtés ils auront donc la même quantité de gâteaux .
en effet , si c est le côté du polygone et H , la distance entre 2 côtés opposés , alors l'aire du gateau est :
A = c/2 x 4H et chacun des enfants en aura la moitié .
par contre , si le polygone est un hexagone ou plus généralement un polygone régulier à 2n côtés avec n impair , alors le plus mal servi aura donc choisi la plus petite hauteur h1 et son copain aura la plus grosse part avec une hauteur H-h1
#16 - 02-01-2015 19:08:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtea u87
Le cas ou le nombre de côtés est multiple de 4 ne semble pas poser problème , on ne peut pas en dire autant pour un simple multiple de 2 
Il faut donc chercher un peu plus loin ( sans calcul ) .
Vasimolo
#17 - 02-01-2015 19:13:01
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gâteau 8
On prend tous les côtés impairs; on forme un nouveau poylgone. Si on place un point dedans, normalement, comme le polygone est régulier, la somme des hauteurs est toujours la même. Ainsi l'aire des triangles ne varie pas, et c'est égal à la moitié de l'aire du polygone
Un promath- actif dans un forum actif
#18 - 02-01-2015 19:56:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
gâyeau 87
C'est bien la 1ère chose que j'ai vue tout de suite, cf msg 2: 2 parts qui partent de 2 cotés opposés ont pour aire la moitié du produit de la largeur d'un coté par la largeur du polygone. Et comme c'est un polygone régulier, toutes les paires ont même aire. Et comme il y a autant de paires rouges que de jaunes, il y a égalité.
#19 - 03-01-2015 00:54:15
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Gâteauu 87
Bonne année !
Peu importe comment on déplace le point sur le gâteau, ce que l'on perd sur une part est gagné par son opposée.
Pour s'en convaincre il suffit de tracer un des axes de symétrie de la figure passants par 2 sommets puis de jouer au tangram dans les 2 demi-figures ainsi formées 
Les deux enfants repartiront donc toujours avec une moitié de gâteau chacun 
#20 - 03-01-2015 09:48:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteua 87
@Promath-: c'est tout bon , il faudrait quand même préciser "on forme un nouveau polygone" .
@Nodgim et Sydre : Le résultat est juste mais les explications peu convaincantes:)
Vasimolo
#21 - 03-01-2015 10:18:26
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
gâyeau 87
On forme un nouveau polygone en prolongant les côtés pairs, comme la propriété est vraie à l'intérieur du polygone à n côtés, elle est vraie aussi à l'intérieur du polygone à 2n côtés
Un promath- actif dans un forum actif
#22 - 03-01-2015 11:53:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
fâteau 87
OK Promath- 
Vasimolo
#23 - 03-01-2015 13:11:05
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
gâteay 87
Y a une histoire de symétrie là dedans, comme disait mon prof de Terminale.
Le point excentré donnera le même résultat pour 2n autres points du polygone (il suffit de tourner le polygone 2n fois pour s'en convaincre). Or, si on prend le symétrique du point excentré par rapport au centre, ce symétrique fait partie des 2n points, il y a non changement de répartition. Mais si on dessine ce symétrique, qu'on rejoint les angles du polygone, par symétrie les triangles rouges et jaunes diamétralement opposés échangent leur aire. Or c'est le même résultat que si on avait tourné le polygone de 180 degrés, mais avec les couleurs inversées: il y a donc égalité des aires.
#24 - 03-01-2015 13:24:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtzau 87
C'est peut-être vrai , Nodgim , mais j'aime tellement quand tout est simple 
Vasimolo
#25 - 03-01-2015 14:04:45
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtea 87
Oui c'est vrai on peut faire plus concis:
Si on intervertit les couleurs ou si on tourne le polygone de 180 degrés, on a la même figure à la symétrie près.
|
 |

 Accueil
Accueil
 Forum
Forum