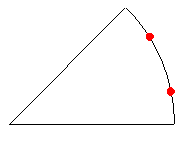
Ne cherche pas trop compliqué , si tu trouves un petit huitième de cercle ( ouvert ) contenant deux points du réseau et dont les rayons sont des axes de symétrie du réseau , tu as fini . Je rappelle que le centre du cercle n'est pas forcément un nœud du réseau .



Et j'ajoute encore un peu de temps pour faire râler Halloduda

Tout le monde doit trouver

Vasimolo

Du coup, nouvelle hypothèse (que j'aurais testée si la première réponse n'avait pas été acceptée ) : le centre de la galette est au centre d'un carreau (on conserve toujours la symétrie globale du quadrillage sur la galette : il y a toujours 4 noeuds par quart de galette).

Avec le même raisonnement que pour ma première réponse, on trouve alors 32,5 (= 1,5*1,5 + 5,5*5,5 = 3,5*3,5 + 4,5*4,5).
Le rayon de la galette est donc de racine de 32,5 côtés d'un carreau (2 cm), donc son diamètre est de 4 racine de 32,5 cm, soit 22,80 cm en arrondissant au mm.

Il fallait donc trouver [latex]\sqrt{520}\approx 22,80.[/latex]

On cherche naturellement une solution ayant des symétries communes avec le quadrillage , sans oublier ( bêtement comme moi ) que le centre du cercle peut aussi être le centre d'une maille .

Je vous renvoie aux solutions et illustrations données ci-dessus .

J'ai pris l'habitude depuis un moment de proposer des gâteaux dont je n'avais pas la solution ( en tout cas pas avec certitude ) . J'ai proposé ici une case réponse en précisant qu'elle validait la meilleure réponse que j'avais trouvée puis j'ai modifié cette case en le notifiant clairement et en précisant mes raisons . Désolé pour la gène occasionnée chez certains , je n'aurais sans doute pas dû proposer de réponse .

En tout cas , merci aux nombreux participants

Vasimolo

PS : la décomposition d'un entier en sommes de carrés est étudiée depuis très longtemps , je trouve que c'est un joli problème aux multiples applications .

Je n'ai pas d'argument définitif mais il est clair que si le centre du cercle est aussi un centre de symétrie du quadrillage alors un nœud en fourni automatiquement 3 ou 7 autres : une bonne raison de commencer par là .

Vasimolo