Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 10-03-2011 17:41:45
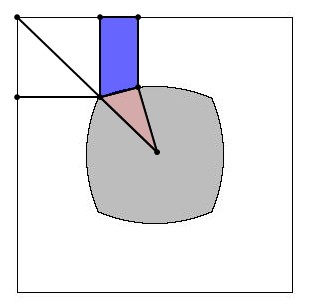
crnter parcLes côtés du carré sont de longueur 1 mètre et la région grise représente l'ensemble des points qui sont plus proches du centre du carré que des côtés. C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#0 Pub#2 - 10-03-2011 20:23:39
centzr parcLes sommets sont à [latex]1-\sqrt2/2[/latex] du centre ce qui determine trois points de l'arc formant le coté du 'blob'. Pythagore nous donne la corde de l'arc qui mesure [latex]\sqrt2-1[/latex] et sa flèche [latex]\frac{3-2\sqrt2}4[/latex]. The proof of the pudding is in the eating. #3 - 10-03-2011 20:28:49
Centerr ParcPour l'aire, je propose : #4 - 10-03-2011 20:51:51
cenyer parcBonne réponse de L00ping et encore une belle solution de Franck. C'est à l'intelligence d'achever l'oeuvre de l'intuition. #5 - 10-03-2011 20:57:22
Center PacLa surface grisée est délimitée par 4 arcs de parabole ayant pour foyer le centre du carré et pour directrices les 4 côtés du carré. #6 - 10-03-2011 22:46:38
Centr ParcLa courbe est formée par 4 morceaux de parabole. #7 - 11-03-2011 03:11:32
center parvj'aime bien tes énigmes, je vais me lancer dans celle ci #8 - 11-03-2011 13:08:49
Center PParc
#9 - 11-03-2011 13:44:18
Center PrcSoit O centre du carré de côté 1 #10 - 12-03-2011 07:05:59
center parxBon alors j'ai une super idée ! #11 - 12-03-2011 14:36:57
xenter parcbon alors si je considère que les points les plus proches du centre que les côtés se trouvent en dessous de R/2 en prenant R la longueur de chaque segment [OA], O le centre, A un point du carré. #12 - 12-03-2011 17:35:08
Center aPrc1) je calcule l'equation du 1/4 de la courbe, et je trouve que la distance A entre la face du haut et le 1/4 de courbe le plus pres est de X^2_0.25, X etant la distance horizontale entre un point quelconque et le centre. Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #13 - 12-03-2011 23:08:59
center parxLe contour de la surface grisée est défini par les homothéties des 4 cotés par apport au centre dans le rapport 1/2, ce qui donne des segments de droites #14 - 12-03-2011 23:10:45
Centre Parc
C'est à l'intelligence d'achever l'oeuvre de l'intuition. Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.