On arrive à démontrer géométriquement que la somme des angles d'un triangle vaut 180° en dessinant les parallélogrames "circonscrits".

Pour un polygone à n côtés, en partant des triangles associés, on arrive à une somme d'angles de: S = n.(180 - 360/n) = 180.n - 360 (pour n>2).

Complément plus détaillé
Je prend un point intérieur au polygone à n côtés et je dessine les n triangles associés en joignant ce point central aux n sommets.
Soient Ai les angles "centraux" de ces n triangles. La somme des angles Ai (i variant de 1 à n) vaut 360° (tour complet) et la somme des deux autres angles de chaque triangle vaut 180° - Ai.
Donc la somme des angles du polygone est la somme des (180° - Ai), ou encore la (somme des 180° - somme des Ai), soit 180.n - 360.

Je l'ai eu en D.S.T cette année et j'ai pu trouver la réponse mais ça m'a pris un peut de temps. Il faut en fait démontrer que la somme des angles d'un triangle est égal à un angle plat qui vaut deux angles droits et donc 2*90 = 180.

On trace un triangle quelconque ABC. On prolonge la droite AB on construisant un point E du côté de B. On construit la droite (BD) parallèle à (AC) passant par B. Puis on utilise deux propriétés :
- Les angles ACB et CBD sont alternes-internes par rapport aux deux droites parallèles et à la sécante (BC) donc ACB = CBD.
- Les angles BAC et DBE sont correspondants par rapport aux deux droites parallèles et à la sécante (AB) donc BAC = DBE.

L'angle ABE est un angle plat et ABE = ABC+CBD+DBE.
Or CBD=ACB et DBE=BAC donc ABE = ABC+ ACB+ BAC donc l'angle plat ABE vaut la somme des angles du triangle ABC.

Voilà. J'espère que j'aie été précis. Et aussi, il faut préciser sur une surface plane car sur une sphère la somme des angles d'un triangle est de 270°. Ça, c'était pour chipoter un peu. Je réfléchis pour le cas d'un polygone à n côtés.

Edit : J'ai trouvé ! En fait la somme des angles d'un polygone à n côtés vaut 180(n-2) car on peut y "loger" n-2 triangles délimités par des diagonales de ce polygone.

Démonstration premier point
Soit le triangle ABC. Si je trace une parallèle au côté [BC] passant par le point A, ces
2 droites parallèles (coupées par la sécante) déterminent des angles alternes-internes qui forment ensemble un angle plat: CQFD.

Bonnes réponses de Franky et Promath !

Théorème 1 : Si une droite coupe deux droites parallèles, alors elle forme des angles alterné égaux.



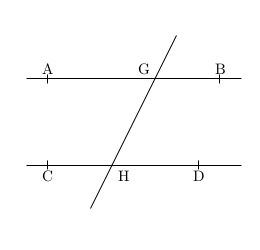
Dans la figure ci-dessus, on veut montrer que l'angle $\widehat{AGH} =\widehat{GHD}$

Si $\widehat{AGH} < \widehat{GHD}$ alors on a :
$$\widehat{AGH} + \widehat{GHC} < \widehat{GHD} + \widehat{GHC} =180°$$
Or d'après le cinquième postulat d'euclide (si une droite coupe deux autres droites alors ces deux dernières droite se rencontre du côté où la somme des angles formés avec la troisième droite est inférieure à 180° ("deux droits")) cela
signifie que (AB) et (CD) se coupent, cela contredit l'hypothèse qu'elle sont parallèles.


Le théorème 1 n'utilisant pas le fait que la somme des angles d'un triangle est
égal à deux droits, je peux l'utilisé :




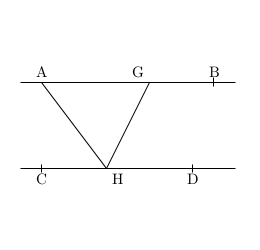
Dans la figure ci-dessus, d'après le théorème 1 on a :
$$\widehat{AGH} = \widehat{GHD}[/latex] et [latex]\widehat{GAH} = \widehat{AHC}$$
Donc $\widehat{AGH} +\widehat{GAH} + \widehat{GHA} = \widehat{GHD} +\widehat{GHA} +\widehat{AHC} = 180°$

Je n'ai pas beaucoup de mérite, j'ai été feuilleté quelques pages de ce livre.
Si vous arrivez un peu à lire l'ancien français c'est très intéressant :
http://gallica.bnf.fr/ark:/12148/bpt6k6 … .f3.langFR

J'ai la flemme de faire des figures. Ce sera donc vite fait sur Paint !

Question 1 : le triangle

Soit ABC un triangle quelconque (on évite le plat). Je trace la parallèle à (BC) passant par A. J'appelle (d) cette parallèle.

Je m'intéresse maintenant à (d). (d) partitionne le plan en deux demi-plans dont l'un contient le triangle ABC au sens large. Intéressons-nous à ce demi-plan et oublions l'autre.

Dans le cas où le triangle ABC est aigu ou rectangle en A.


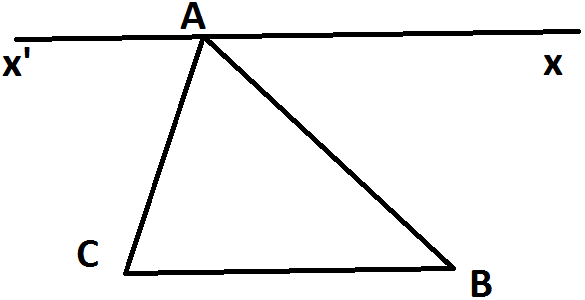
N'est-il pas beau ?

J'appelle x "l'extrémité" de (d) telle que l'angle BAx soit aigu, et j'appelle x' l'autre extrémité de (d).

Ainsi, les angles xAB et CBA sont alternes-internes.
En outre, les angles x'AC et ACB sont alternes-internes.

On a donc : BAC + ACB + CBA = BAC + x'AC + xAB (les quantités additionnées sont des angles non orientés).

Or, BAC + x'AC + xAB = x'Ax = 180°

Donc BAC + ACB + CBA = la somme des angles d'un triangle = 180°

Dans le cas où le triangle ABC est obtus.

Je conserve les mêmes notations pour x et x'.

Cette fois-ci, on a : xAC = ACB et x'AB = ABC. Avec le même raisonnement, on retrouve la propriété à démontrer.

Dans le cas où le triangle ABC est rectangle en B (en C).

J'appelle x' l'extrémité de (d) telle que x'AC est aigu.

Si ABC rectangle en C : J'appelle x l'extrémité de (d) telle que xAB aigu.

Même raisonnement, la propriété est démontrée.



Question 2 : la somme des angles d'un polygones à n côtés.

J'appelle A(n) la somme des angles d'un polygone à n côtés en degrés.

Et là, ça se corse... Je me rends compte que définir un A(n) en général pour un polygone quelconque à n côtés n'est pas valide, puisqu'il existe des polygones croisés qui sont donc particulièrement embêtants. En plus la manière dont la question est posée inviterait à y réfléchir... (enfin j'espère mal comprendre )

Bref, pour l'instant, définissons A(n) seulement pour les polygones non croisés.

A(3) = 180 ; et, au vu de la valeur des sommes des angles d'un carré, d'un pentagone régulier et d'un hexagone régulier, je suppose que :

A(n) = 180(n-2) pour n supérieur ou égal à 3.

Pour un polygone convexe à n+1 côtés :

Soient A, B et C trois sommets consécutifs de ce polygone. Les arêtes [AB] et [BC] sont donc tracées.

Je trace l'arête [AC]. J'ai donc d'un côté un polygône à n côtés, et de l'autre, un triangle ABC. Les deux figures ont pour côté commun [AC].


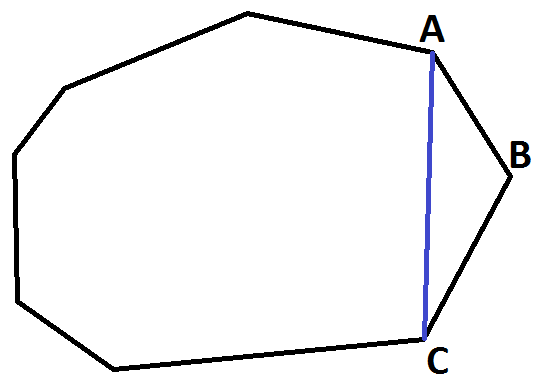
Ce polygone noir est à (n+1) côtés, oui oui oui.

L'hypothèse de récurrence est : A(n) = 180(n-2).

En outre, A(3) = 180 (question 1).

A(n+1) = A(n) + A(3) (on pourrait le détailler en prenant sur la figure les sommets voisins de A et C (autres que B) et en faisant un calcul d'angles).

D'où A(n+1) = 180(n-1). Par récurrence, propriété démontrée !

Pour un polygone non convexe :

Je prends un polygone à n côtés que j'appelle Pn. Il est quelconque mais, bien sûr, pas croisé.

Je suppose qu'il a au minimum 4 points, le cas triangle ayant été traité.

J'appelle S1, S2, S3, S4, ..., Sn les n sommets du polygone Pn. (n étant supérieur ou égal à 4, il est possible d'avoir en fait Sn = S4)

Enfin, je suppose sur Pn que [S1S3] n'appartient pas au polygone Pn. Pn est donc non convexe (problème "en S2").

Je prends un point T dans le plan tel que :
- le polygone S1.T.S3.S4...Sn.S1 soit non croisé ;
- T n'appartienne pas à [S1S3] ;
- la diagonale [S1S3] appartienne au polygone S1.T.S3.S4...Sn.S1.


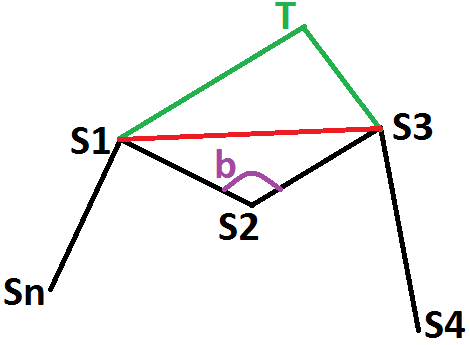
Bon là, ça fait polygone à n côtés, non ??

Soit Qn le polygone S1.T.S3.S4...Sn.S1. Qn est peut-être encore non convexe, mais ce ne sera pas "en T".

Mon objectif est de montrer que la somme des angles du polygone Pn est la même que la somme des angles du polygone Qn.
C'est équivalent à montrer l'égalité sur ces sommes d'angles :
SnS1S2 + S1S2S3 + S2S3S4 = SnS1T + S1TS3 + TS3S4 (1) .
Montrons donc (1).

On notera bien qu'on parle d'angles du polygone. Ils peuvent être supérieurs à 180° car on prend les angles intérieurs au polygone. Dans la suite, les angles écrits seront des angles intérieurs à leurs polygones.

L'angle S1S2S3 est donc supérieur à 180° et vaut S1S2S3 = 360° - b.

Le quadrilatère S1.T.S3.S2 est, par construction, convexe donc la somme de ses angles vaut 360° (démontré plus haut).
Or, puisque le quadrilatère S1.T.S3.S2 est non croisé on a donc aussi :
360° - b = S2S1T + S1TS3 + TS3S2. Donc :
S1S2S3 = S2S1T + S1TS3 + TS3S2 (2)

On calcule le membre gauche de l'égalité à démontrer (1) en utilisant (2) :

SnS1S2 + S1S2S3 + S2S3S4 = SnS1S2 + S2S1T + S1TS3 + TS3S2 + S2S3S4
Les termes soulignés vont ensemble :
SnS1S2 + S1S2S3 + S2S3S4 = SnS1T + S1TS3 + TS3S4

(1) est donc montré.

Ainsi : en prenant P'n un polygone non convexe quelconque à n côtés, il est toujours possible de montrer que la somme de ses angles est égale à celle d'un polygone convexe à n côtés (par transformations successives, en faisant intervenir plusieurs points T. Remarquez que les valeurs de SnS1S2 et S2S3S4 peuvent être quelconques, Pn aurait très bien pu être non convexe "en S1" ou "en S3").


Donc, pour tout polygone non croisé à n côtés, la somme de ses angles vaut toujours 180(n-2) degrés.

Ouf !

Et pour les polygones croisés, on verra !

Alexein41

Pardon, j'avais oublié le cas général :

Pour un polygone à n coté la somme des angles est (n - 2) * 180.
Pour s'en rendre compte on peut relié un sommet à tous les autres, et on voit apparaître (n - 2) triangles et la somme des angles de ces (n-2) triangles est
la somme des angles du polygone .

Bonne réponse de Cogito !

Pour le cas des polygones croisés, on doit pouvoir faire par récurrence :

Pour un quadrilatère croisé on obtient une forme avec deux triangles (comme les deux ailes d'un papillon), donc la somme des angles est 2 * 180.

Si on a un polygone croisé à n côtés, alors aux croisement on peut "coupé" ce polygone pour obtenir deux polygones : un avec k côtés l'autre avec n - k + 2 côtés.

Comme ce sont des polygones avec un nombre plus petit que n de côtés, on peut appliquer l'hypothèse de récurrence sur chacun de ces polygones.

Donc la somme des angles du polygone à k côtés est (k-2) * 180 et la somme des angles de l'autre polygone est (n-k+2-2) * 180 = (n-k) * 180.

Ainsi la somme des angles du polygone à n côtés est :
(n - k) * 180 + (k - 2) * 180 = (n - 2) * 180.

Donc finalement le théorème est vrais aussi pour les polygones croisés.

Sauf qu'il y a une ambiguïté dans la définition d'un angle d'un polygone croisé !

Par exemple, si je prends le quadrilatère croisé suivant :



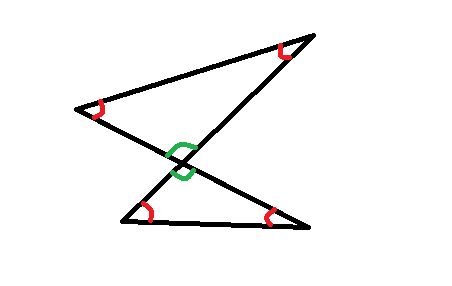
Faut-il comprendre par "somme des angles" la somme des angles en rouge ou la somme des angles en rouge ET en vert ?

Un angle d'un polygone étant délimité par deux côtés consécutifs, il me semblerait plus naturel de ne considérer que les angles en rouge...

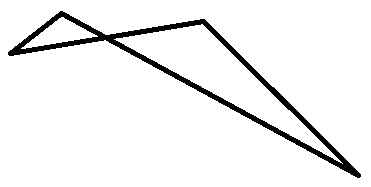
EDIT : Nombrilist m'a devancé ! Enfin, les angles ne sont pas tous nécessairement aigus !

shadock a écrit:

La somme des angles d'un triangle fait 180° :
Démonstration :
Dans le triangle ABC, on a les angles orientés suivant :

(CA;CB) (AB;AC) et (BC;BA)
Donc d'après la relation de Chasles on a:
(CA;CB) + (AB;AC) + (BC;BA) = (AB;BA)
Les vecteurs AB et BA sont colinéaires et de sens opposés, donc  (AB;BA) = 180°

Cette démonstration n'est pas complète, car en raisonnant avec des angles orientés et non des angles géométriques, le résultat obtenu l'est modulo 360°.