Enigme Le vieux dossier de Grand-Père : N°5 @ Prise2Tete

kossi_tg · #1

Salut à tous,
Une feuille rectangulaire de longueur L et de largeur l est pliée suivant une de ses diagonales pour donner la figure ci-dessus.

Quel est le périmètre p du pentagone ABCDE en fonction de L et l?

Application numérique: L=70 et l=45. Réponse à valider dans la case réponse avec 3 chiffres après la virgule. Utilisez le point comme séparateur décimal.

Merci pour votre participation.

Franky1103 · #2

Par symétrie, on a: BC=CD, que l'on va appeler x.
Le triangle ABC est rectangle en B: on a donc:
(L-x)²=x²+l², ce qui donne x=L/2-l²/2L
Le périmètre vaut donc: P=V(L²+l²)+2l+L-l²/L
AN: L=70 et l=45 donnent P=214.288 env.
Merci pour ces petites énigmes sympathiques.

nolina · #3

Désolée, je ne sais pas me servir d'un clavier... Toutes mes racines carrées seront donc écrites comme ceci : V(...) . Et mes carrés seront : {2}

Le périmètre de ce pentagone est égal à AB+BC+CD+DE+EA.
*DE = AB = l
*Le triangle ABE est rectangle. Donc d'après le théorème de Pythagore:
AE= V(L{2}+l{2})
* On sait que CD=BC Appelons cette longueur x.
dans le triangle CDE, rectangle en D
CE{2}=DE{2}+CD{2}
(L-x){2}=l{2}+x{2}
L{2} - 2xL + x{2} = l{2}+x{2}
2xL=L{2} - l{2}
x= (L{2} - l{2})/2

Donc P(ABCDE)= 2l + (L{2} - l{2}) + V(L{2}+l{2})

Avec l'exemple numérique P(ABCDE) = 214,288

cogito · #4

Bonsoir

Le périmètre du pentagone ABCDE est AB + BC + CD + DE + EA.

Nous avons [latex]AB = DE = l[/latex]

Pythagore donne [latex]EA = \sqrt{L^2+l^2}[/latex].

Les triangles ABC et EDC sont isométriques (car ils ont leurs angles égaux et les côtés AB et ED de même longueur). Donc en particulier BC=CD.

Posons donc [latex]x=BC=CD[/latex].2*45 + 70 - {45^2\over70} +\sqrt{45^2 + 70^2}

Le périmètre de ABCDE est donc :
[TeX] l + x + x + l + \sqrt{L^2+l^2} = 2(l+x) +\sqrt{L^2+l^2}[/TeX]
Pythagore dans ECD, par exemple donne :
[TeX]x^2+l^2 = (L-x)^2[/TeX]
[TeX]\Leftrightarrow x^2 + l^2 = L^2 -2Lx + x^2[/TeX]
[TeX]\Leftrightarrow l^2 = L^2 -2Lx[/TeX]
[TeX]\Leftrightarrow x = {L^2 - l^2\over 2L}[/TeX]
Ce qui fait que le périmètre de ABCDE est :
[TeX]2(l+{L^2 - l^2\over 2L}) +\sqrt{L^2+l^2} = 2l + L -{l^2\over L}+\sqrt{L^2+l^2}[/TeX]
Donc pour L=70 et l = 45 , le périmètre de ABCDE est :
[TeX]2*45 + 70 - {45^2\over70} +\sqrt{45^2 + 70^2} = 160 - {45 * 9\over 14} + \sqrt{2025 +4900}[/TeX][TeX]= 160 - {405\over 14} + 5\sqrt{277} \simeq 214,288[/TeX]
Voilà .

kossi_tg · #5

Que de bonnes réponses
BRAVO à tous!

masab · #6

La réponse est [latex]214.288[/latex]
Plus précisément le périmètre est donné par la fonction
[TeX]P(L,l)=2l+\frac{L^2-l^2}{L}+\sqrt{L^2+l^2}[/TeX]
Or [latex]P(70,45) = 214.288013456894...[/latex]
Voilà !

Preuve
On pose [latex]\tan a=\frac{l}{L},\ \tan b=\frac{L}{l}\ \ [/latex] donc [latex]a+b=\frac{\pi}{2}[/latex] .
Alors
[TeX]BC=l\,\tan(b-a)=l\,\frac{\tan b -\tan a}{1+\tan a\tan b}[/TeX][TeX]BC = l\,\frac{\frac{L}{l}-\frac{l}{L}}{1+\frac{l}{L}\frac{L}{l}} = \frac{L^2-l^2}{2L}[/TeX]
De plus par Pythagore [latex]AE=\sqrt{L^2+l^2}[/latex]
Donc
[TeX]P(L,l)=2\,AB+2\,BC+AE[/TeX]
[TeX]P(L,l)=2\,l+\frac{L^2-l^2}{L}+\sqrt{L^2+l^2}[/TeX]
[TeX]\square[/TeX]

JulesV · #7

Notons x la longueur BC.
Étant donné que la symétrie conserve les angles, ACB et ECD sont des triangles de même longueur (on peut le montrer juste en considérant l'angle droit et les deux angles du triangle rectangle), on a [latex]x=BC=CD[/latex].

On a aussi:

AB²+CD²=(AD-CD)²

soit
[TeX]l²+x²=(L-x)²[/TeX]
soit
[TeX]x= \frac{L²-l²}{2L}[/TeX]
Finalement, [latex]p=\sqrt{L²+l²}+2l+\frac{L²-l²}{L}[/latex]

Avec [latex]l=45[/latex] et [latex]L=70[/latex],
[TeX]p=5\sqrt{277}+\frac{1835}{28} \simeq 214.288[/TeX]

kossi_tg · #8

BRAVO à tous!

gwen27 · #9

AE=rac(L^2 +l^2)
AB=ED=l

BC=CD=x

(L-x)^2 = l^2 +x^2
L^2-2Lx+x^2=l^2+x^2
x=(L^2 - l^2)/2L

Périmètre : rac (l^2+L^2) +2l + (L^2-l^2)/L

L=70
l=45

P = 83,21658488+90+41,0714285714= 214,288

kossi_tg · #10

BRAVO à tous et MERCI pour votre participation

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 08-09-2013 18:33:00

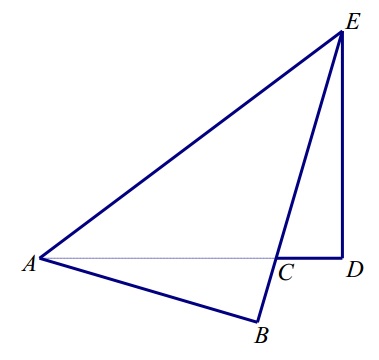
Le vieux dosier de Grand-Père : N°5

#0 Pub

#2 - 08-09-2013 19:17:47

lr vieux dossier de grand-père : n°5

#3 - 08-09-2013 21:00:02

Le vieux dossier d Grand-Père : N°5

#4 - 08-09-2013 21:23:26

Le vieux dossier de Grand-Père N°5

#5 - 08-09-2013 21:49:33

Le viexu dossier de Grand-Père : N°5

#6 - 09-09-2013 12:31:17

le vieux dossiet de grand-père : n°5

#7 - 09-09-2013 16:58:45

Le vieux dosseir de Grand-Père : N°5

#8 - 09-09-2013 22:42:03

le vieux dodsier de grand-père : n°5

#9 - 11-09-2013 11:36:13

Le vieux dossier de Grnd-Père : N°5

#10 - 11-09-2013 19:06:36

Le vvieux dossier de Grand-Père : N°5

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums