|
#26 - 19-12-2015 00:41:55
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
Gâteau 1114
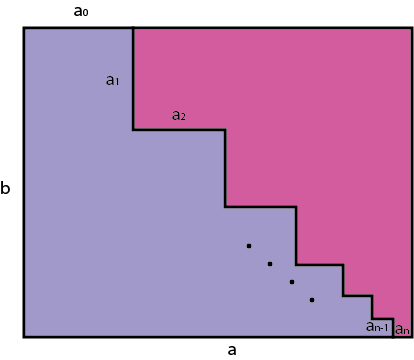
Si on veut que les formes soient semblables on a comme contraintes :
. [latex]a_{n+1}\ =\ k\ a_n [/latex] où [latex]k[/latex] est le coefficient de réduction [latex]k\in [0,1] [/latex]
. [latex]a\ =\sum\limits_{i=0}^{n/2} a_{2i} [/latex]
. [latex]b\ =\sum\limits_{i=0}^{n/2-1} a_{2i+1} [/latex]
(j'omets deux contraintes sur les grands cotés parce qu'elles sont liés aux contraintes sur les marches de l’escalier par des sommes simples)
Il s'agit de trouver un [latex]n[/latex] et un [latex]k[/latex] qui conviennent pour [latex]a[/latex] et [latex]b[/latex] fixés [latex]a > b[/latex].
Il suit immédiatement
. [latex]a_n=\ k^na_0 [/latex]
. [latex]a\ =\ \frac{1-k^{n+2}}{1-k^2}a_0 [/latex]
. [latex]b\ =\ \frac{k-k^{n+1}}{1-k^2}a_0 [/latex]
en éliminant [latex]a_0[/latex] on obtient un polynôme en [latex]k[/latex] de degré [latex]n[/latex] qu'il suffit d'annuler pour que ça marche :
[TeX]\boxed{f(k)\ =\ bk^{n+2}-ak^{n+1}+ak-b}[/TeX]
[TeX]f(0)=-b [/TeX]
[TeX]f(1)=0 [/TeX]
La dérivé en 1 est :
[TeX]f'(1) = (n+2)b-(n+1)a+a \\ = 2b - n(a-b)[/TeX]
donc pour [latex]\boxed{n > \frac{2b}{a-b}}[/latex] on a [latex]f'(1) < 0[/latex]
Ce qui nous garantis l’existence de valeur positive de [latex]f(k)[/latex] au voisinage de 1, puis l’existence d'au moins une racine [latex]k_0[/latex] dans [latex]]0,1[[/latex] en appliquant le théorème des valeurs intermédiaires.
Reste le cas du carré [latex]a=b[/latex], la méthode ne marche plus (on converge vers une diagonale, en effet [latex]a=\frac{b}{k}+a_n > b[/latex] on se rapproche de l'égalité si [latex]k[/latex] tend vers 1, et [latex]n[/latex] vers l'infinie pour annuler [latex]a_n[/latex]). Ma solution précédente avec une infinité de segment peut être utilisée en consolation 
#27 - 19-12-2015 05:41:04
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâteau 14
Je n'avais pas considéré la possibilité d'une tatin ce qui explique peut être ma mauvaise réponse.
Dans ce cas je propose que tout les rectangles fonctionnent par homothetie de rapport 0 entre un point du rectangle et son complémentaire..
Ca va plaire à ceux qui ont débattu sur le 113...
#28 - 19-12-2015 09:32:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
hâteau 114
@Mathieu : c'est ça . Pour être complet il faudrait expliquer pourquoi ce n'est pas possible avec un gâteau carré .
@Portugal : on cherche plutôt une similitude indirecte .
Vasimolo
#29 - 19-12-2015 10:07:37
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
âteau 114
salut.
je ne comprend car #12 j'ai une similitude avec 2 rectangles quand L>2l
#24 j'ai une similitude indirecte avec 2 hexagones concaves.
que j'ai même généralisée avec des polygones pairs concaves, quand L<2l
que doit-on trouver? ta solution avec ton rapport de similitude?
Faute de réponses , je laisse tomber.
#30 - 19-12-2015 10:08:51
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Gâteau 11
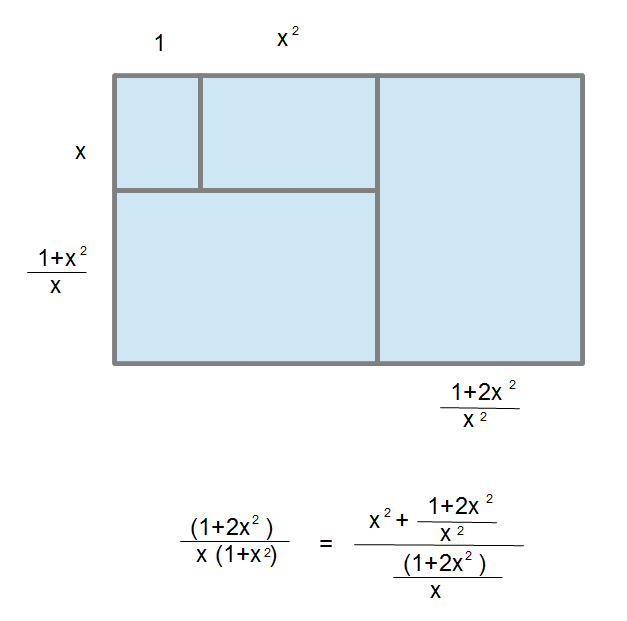
J'en trouve un de ce genre-là...
Par contre, je n'ai pas résolu l'équation, mais par dichotomie, x ressemble fort à la racine du nombre d'or. 1,27202... =racine (1,618...)
#31 - 19-12-2015 10:32:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âteau 114
@Une coudée : je ne vois pas comment tu résous le problème dans tous les cas : si tu pouvais faire une petite synthèse ( sinon laisse tomber  ) )
@Gwen : tu n'as pas tout à fait le bon angle d'attaque ( mais tu n'es pas loin ) .
Vasimolo
#32 - 19-12-2015 10:40:33
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâteua 114
il me semble avoir été clair .j'ai argumenté mathématiquement. je laisse donc tomber la patisserie.
i
#33 - 19-12-2015 10:48:29
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâetau 114
@Unecoudée : tu fais comme tu le sens , je n'ai simplement pas compris tes arguments 
Vasimolo
#34 - 19-12-2015 21:01:08
- Fred11
- Amateur de Prise2Tete
- Enigmes résolues : 47
- Messages : 1
gâtrau 114
Si on a un gâteau qui fait 15 par 6, on fait une part de 12 par 6 et une autre part de 6 par 3 (50% de la première part).
En les assemblant, on a un gâteau rectangulaire de 15 (12+3) par 6.
#35 - 20-12-2015 11:32:34
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
fâteau 114
On découpe le rectangle en 1 (partie) réduite et 1 (partie) résiduelle.
La réduite ne peut être une enclave du rectangle. Elle occupe donc une partie du périmètre du rectangle.
Elle ne peut occuper un coté long en entier, sinon elle serait aussi longue que la résiduelle. Elle ne peut donc occuper que soit une partie d'un coté, soit une partie de 2 cotés consécutifs, soit la totalité du coté court et une partie de chaque coté long.
La réduite ne peut être un convexe sur un seul coté ou dans un seul angle du rectangle. Car ce convexe crée du concave dans la résiduellle. On ne peut pas reproduire ce concave dans la réduite pour tenter de le compenser, car alors on créerait un convexe relativement plus petit dans la résiduelle, qu'il faudrait à nouveau reproduire dans la réduite, etc...
La réduite doit donc occuper 2 angles du rectangle. Le coté court du rectangle ne peut être que sa longueur. La réduite est donc une copie de la résiduelle tournée à 90°. On en arrive donc à la découpe droite parallèle au coté court du rectangle. Si on découpe autrement qu'en ligne droite, cette découpe se trouve sur la longueur de la réduite, mais sur la largeur de la résiduelle, ce qui donnerait 2 formes différentes.
Au final, il n'y a que la solution de découpe en 2 rectangles, quand on peut le faire.
#36 - 20-12-2015 13:30:27
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
gâreau 114
Hello
Je dirais n'importe lesquels:
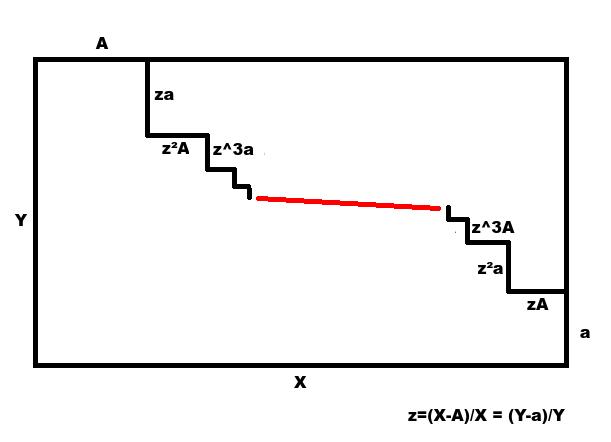
X et Y sont fixés, A est un paramètre libre (a s'en déduit). A priori il suffit de choisir A pour que les deux escaliers convergent dans le rectangle et qu'on puisse tracer par exemple une droite entre ces deux foyers pour achever la pièce. (J'ai la flemme de calculer comment ça converge, mais comme tu poses la question et qu'il me semblerait très difficile de démontrer une réponse autre que "c'est toujours faisable" j'en conclus qu'on peut trouver un A qui convient :p)
Petite correction:
Contrairement a ce que j'ai dit, on ne peut pas bêtement finir par un segment entre les 2 foyers, donc il faut finir avec les deux foyers confondus. Donc faut faire le calcul. Je le ferais asap.
Calculs:
Il semblerait que quelque soit la valeur choisie de A les deux escaliers convergent miraculeusement vers le même point. Donc ça marche toujours.
#37 - 20-12-2015 18:23:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtea u114
@Fred : oui et il y en a beaucoup d'autres .
@Nodgim : si , ça existe mais les parts sont indirectement semblables ( comme dans un miroir ) .
@Clydevil : il y a beaucoup de paramètres dans tes calculs mais ça semble marcher ( essaie plutôt de prendre le problème dans l'autre sens en construisant le rectangle à partir du découpage ) .
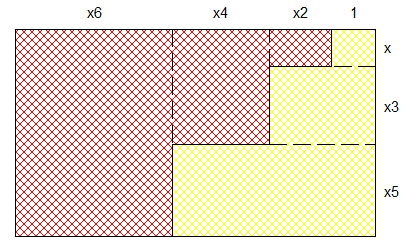
Je pensais que le problème était très facile mais apparemment il surtout facile de s'y perdre . La solution que j'ai est constituée de deux parts en escalier comme sur le dessin de présentation mais avec des marches de tailles différentes .
Bon courage à ceux qui cherchent encore 
Vasimolo
#38 - 20-12-2015 19:43:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtezu 114
@Unecoudée : Je ne fais pas beaucoup d'effort ( je viens seulement de découvrir que tu avais édité ton message #24 ) . J'ai un peu de mal à voir à quel moment tu récupères les quasi-carrés .
Vasimolo
#39 - 21-12-2015 09:33:34
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
gâteai 114
bonjour.
et j'ajouterai qu'avec ce cas de figure , le rapport limite est atteint avec k=0.6180339887.. l'inverse du nombre d'or ; mais dans ce cas l'escalier est infini , les dernières marches n'étant plus visible .
un autre exemple pour obtenir un gâteau proche d'un carré
avec un rapport k = 0.95 donc proche de 1
le rectangle mesure 4.115518.. x 3.27949..
j'obtiens deux polygones à 10 côtés , donc 2 escaliers de 4 marches.
le plus petit possède les côtés suivant:
avec a = 3.27949..
[TeX]a , ak , k , k^2 , k^3 , k^4 , k^5 , k^6 , k^7 , k^8[/TeX]
le plus grand possède les côtés suivant:
[TeX]\frac{a}{k} , a , 1 , k , k^2 , k^3 , k^4 , k^5 , k^6 , k^7 [/TeX]
leur rapport de similitude est bien k = 0.95
avec un rapport k=0.9999999.. on est quasi carré mais non carré.
#40 - 21-12-2015 12:03:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 141
Ce que tu appelles le rapport limite c'est k=largeur/longueur ?
Vasimolo
#41 - 21-12-2015 12:24:07
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâtea 114
avec 1/k = L/l = nombre d'or , l'escalier est infini et c'est le seul cas , à mon humble avis.
par contre je n'ai pas eu la réponse à mon poste 12 pour un gâteau long.
qui respecte aussi l'hypothèse de départ qui demande une forme indéterminée de part de gâteau. donc ça fonctionne pour tout rapport 0.6180339..< k=l/L <1 pour les parts en escalier
et 2<k pour les parts rectangulaires
#42 - 21-12-2015 18:36:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#43 - 22-12-2015 10:29:49
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
gâteai 114
Bien joué les gars !
Je suis allé trop vite en retournant la part dans ma tête (au risque de me vriller les neurones !) 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#44 - 22-12-2015 12:42:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteu 114
Limpide le dessin de Vasimolo !
#45 - 22-12-2015 15:52:08
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
hâteau 114
"Yapluka" le découper, ce gâteau. Question probablement bête: le trait de coupe est-il fini ou infini ?
#46 - 22-12-2015 18:02:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtau 114
Il est clairement fini mais a-t-il une limite quand le rectangle tend vers le carré ?
Formulation plus claire du problème : quelle est la longueur limite de la coupe quand la largeur du rectangle tend vers sa longueur donnée ?
Vasimolo
#47 - 22-12-2015 18:18:13
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gtâeau 114
Il est clair que la longueur de la coupe ne peut être supérieure au demi périmètre du rectangle.
#48 - 22-12-2015 18:31:32
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
âteau 114
C'est vrai, donc question effectivement bête. 
#49 - 22-12-2015 19:23:38
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâetau 114
unecoudée a écrit:avec un rapport k=0.9999999.. on est quasi carré mais non carré.
Si, on est carré, puisque 0,999...=1
Mais dans ce cas, on sort des contraintes de l'énoncé qui exige des figures de taille différente.
#50 - 23-12-2015 11:51:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteua 114
Pour répondre à la question que je posais au message #46 , la coupe limite tend vers le demi-périmètre du rectangle quand celui-ci s'approche du carré . En effet le "1" de mon dessin devient alors négligeable devant les côtés du gâteau .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum