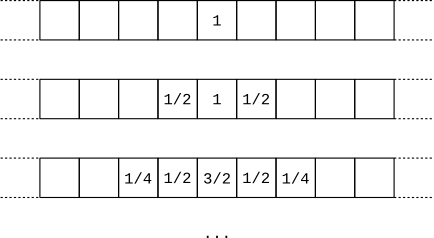
Enigme Le plombier de l'infini @ Prise2Tete

Ebichu · #1

Bonjour à tous. Le groupe sécurité de mon chauffe-eau fuit, et ça m'agace, alors plutôt que de m'occuper du problème, je préfère en tirer une énigme.

Suite à une fuite, une goutte tombe régulièrement dans une gouttière. La gouttière est assimilée à une succession de cases, infinie tant à gauche qu'à droite (voir figure ci-dessous).

À l'instant t=0, toutes les cases sont vides. À l'instant t=1, une goutte est tombée dans la case centrale, et les autres cases sont vides. Puis à chaque nouvel instant, une goutte supplémentaire se rajoute à la case centrale, tandis que par ailleurs, l'eau s'étale : si une case contenait g gouttes, à l'instant suivant, ces g gouttes disparaissent de cette case en se répartissant équitablement dans les deux cases voisines, dont le total augmente ainsi de g/2.

En guise d'exemples, voici la situation aux instants t=1, 2 et 3 :

Lorsque t augmente, on a donc une quantité illimitée d'eau qui va se répartir dans un nombre illimité de cases. Or, on m'a appris en terminale que pour le calcul de limites, "∞/∞" est une forme indéterminée : étant donnée une case de ma gouttière, on peut donc imaginer que le nombre qu'elle contient ait une limite finie, ou que cette limite soit +∞, ou même qu'elle n'ait pas de limite.

Pouvez-vous déterminer le comportement de chaque case de la gouttière : admet-elle une limite, et si oui, laquelle ?

nodgim · #2

Je crois que ça va déborder....

La 1ère goutte seule, au bout de k itérations, se répartit sur 2k-1 cases. Si on double les valeurs dans chaque case (pour éviter les fractions), celles ci correspondent, pour celles qui sont occupées (tantôt paires, tantôt impaires), aux différentes valeurs du binome de Newton.
La 1ère goutte se répartit sur 2k-1 cases
La 2ème sur 2k-3
La 3ème sur 2k-5
La kième sur la seule case centrale.

Donc pour la case centrale, on peut compter la quantité de liquide : Somme(de k=0 à l'infini) C(2k,k) / 2^(2k)

Le rapport entre 2 valeurs successives de cette somme vaut C(2k, k) / (4*C(2k-2,k-1) > 1 / (k+1) si C(2k-2,k-1) / 2^(2k-2) >= 1 / k, ce qui est vrai pour les premières valeurs.

La somme en question est donc > 1 + 1 / 2 + 1 / 3 + 1 / 4....qui diverge.

Donc dans la case centrale, ça va déborder quelle que soit la taille du récipient.

Comme la case voisine contient au moins autant que la moitié de la case centrale, ça va déborder également.

Et la case suivante également, et n'importe quelle case aussi éloignée de la case centrale fut elle.

Ebichu · #3

@nodgim : bravo ! concernant le calcul du milieu de ta preuve, j'avais un argument plus rapide, utilisant un résultat connu mais compliqué à démontrer. J'aime autant ta méthode.

Ebichu · #4

Merci à nodgim pour sa participation. J'avais fait le même raisonnement que lui, si ce n'est que pour établir la divergence de la somme, j'utilisais la formule de Stirling qui donne que C(2k,k) / 2^(2k) ~ 1/racine(kπ), d'où la divergence.

https://fr.wikipedia.org/wiki/Formule_de_Stirling

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 06-02-2018 22:29:02

Le plombier de l'infiin

#0 Pub

#2 - 07-02-2018 15:13:18

Le plombier de l'infinni

#3 - 07-02-2018 18:36:13

Le lpombier de l'infini

#4 - 13-02-2018 19:59:43

Le plobier de l'infini

Réponse rapide

Sujets similaires

Pied de page des forums