Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 16-06-2011 19:30:09
mathématiqyes pour les nuls 9Il me semble qu'il y en a qui voulait plus de difficulté, mais c'est difficile de faire difficile je trouve. Entre deux textes de français j'ai réfléchis pour vous trouver quelque chose qui j'espère sera plus problématique "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#0 Pub#2 - 16-06-2011 20:08:33
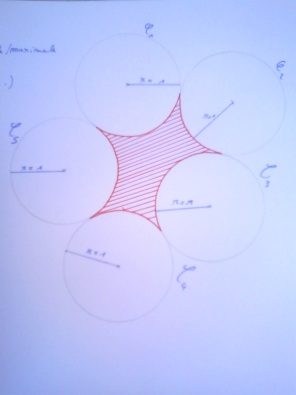
mathématiques pour les nils 9Les centres des cinq cercles de rayon forment un pentagone regulier de cote 2. The proof of the pudding is in the eating. #3 - 16-06-2011 23:01:18
Mathhématiques pour les nuls 9Les centres des cercles forment un pentagone. Il me semble que la surface rouge est maximale si la surface du polygone est maximale. Et donc lorsqu'il est régulier. Il reste plus qu'à calculer (demain). #4 - 17-06-2011 10:11:06
Maathématiques pour les nuls 9Question 1. #5 - 17-06-2011 11:13:55
Mathématiques pour lles nuls 9si on dessine le pentagone formé par les centres des cercles, l'aire rouge est égale a l'aire de ce pentagone moins l'aire d'un cercle et demi (la somme des angles d'un pentagone est constante) #6 - 17-06-2011 12:23:20
mathématiques poyr les nuls 9Bonjour, #7 - 17-06-2011 23:58:44
marhématiques pour les nuls 9J'espère que ça ne vous prend pas trop la tête "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #8 - 18-06-2011 01:47:17
Mathéématiques pour les nuls 91er question: #9 - 18-06-2011 10:56:37
Mathématiques opur les nuls 9Pourquoi est ce que le pentagone donne l'aire maximale ? #10 - 19-06-2011 16:04:38
Mathématqiues pour les nuls 9Je me place dans le plan complexe. Un mathématicien complet est topologiquement fermé! #11 - 21-06-2011 22:32:30
Mathématiques pour les nulsBon cette énigme n'aura pas eu grand succès mais peut être qu'un jour les recherches de certains s'il y en a aboutirons à quelque chose de concret "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.